题目内容
18．
(苏北三市14分) 如图甲所示，一边长L=2.5m、质量m=0.5kg的正方形金属线框，放在光滑绝缘的水平面上，整个装置放在方向竖直向上、磁感应强度B=0.8T的匀强磁场中，它的一边与磁场的边界MN重合。在水平力F作用下由静止开始向左运动，经过5s线框被拉出磁场。测得金属线框中的电流随时间变化的图像如乙图所示，在金属线框被拉出的过程中。
⑴求通过线框导线截面的电量及线框的电阻；
⑵写出水平力F随时间变化的表达式；
⑶已知在这5s内力F做功1.92J，那么在此过程中，线框产生的焦耳热是多少？
 |
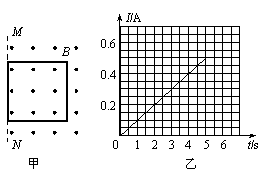解：⑴根据q =
t，由I－t图象得：q =1.25C （2分）
又根据＝
＝
（2分）
得R = 4Ω （1分）
⑵ 由电流图像可知，感应电流随时间变化的规律：I＝0.1t （1分）
由感应电流
，可得金属框的速度随时间也是线性变化的，
（1分）
线框做匀加速直线运动，加速度a = 0.2m/s2 （1分）
线框在外力F和安培力FA作用下做匀加速直线运动，
（1分）
得力F＝（0.2 t＋0.1）N （1分）
⑶ t＝5s时，线框从磁场中拉出时的速度v5 = at =1m/s （1分）
线框中产生的焦耳热
J （3分）
感悟与反思：
这道题精彩之处在于通过给出感应电流随时间做正比例变化，倒推出运动性质为匀变速运动，结合牛顿第二定律解出相关物理量。难度适中，所考查的知识点也不少。另外，学生计算焦耳热时可能会错误地应用平均值概念，这是具有迷惑性的地方。
名题训练系列答案
期末集结号系列答案