Question

灵溪（约27°N）一开阔平地上，在楼高为Ｈ的楼房北面盖新楼与之平行，欲使新楼底层正午太阳光线全年都不被遮挡，两楼距离应不小于：

1. A.
   Ｈ tan（９０°—27°）
2. B.
   Ｈ tan（９０°—27°—２３.5°）
3. C.
   Ｈ/tan （９０°—27°+２３.5°）
4. D.
   Ｈ/tan （９０°—27°—２３.5°）（提示：tan表示正切函数）

Answer 1

D
试题分析：欲使新楼底层正午太阳光线全年都不被遮挡，需考虑冬至日时27°N对应的正午太阳高度，其大小为（90°—27°—２３.5°），则两楼距离L为Ｈ/tan （９０°—27°—２３.5°）。
考点：本题考查正午太阳高度的应用。
点评：本题难度较小，解答本题的关键是明确正午太阳高度的计算公式，明确北回归线以北地区建房时，为保证一楼全年均有阳光照到，两楼之间的最短距离与楼高的关系应满足 L≥h×cotH。（h为楼高，H为冬至日当地的正午太阳高度）。
【重难突破】
1．正午太阳高度的变化与综合运用
（1）太阳高度（角）与正午太阳高度（角）
太阳光线与地平面之间的夹角叫太阳高度（角）。太阳高度角在正午（地方时12时）达到一天中的最大值，叫正午太阳高度（角）。
（2）①纬度分布规律：由直射点所在纬线向两边递减。如下图。

②季节变化规律：太阳直射点靠近时变大，远离时变小。
（3）正午太阳高度计算：某地、某日正午太阳高度H＝90°—纬度差， “纬度差”是指该地所在纬线与该日直射点所在纬线之间的纬度距离。
（4）正午太阳高度的综合运用
Ⅰ．日影的方向和长度的问题：日影方向与太阳光线方向相反。
①日出日落前后太阳光的来向。
除极昼、极夜范围外，其余纬度：3月 21至 9月 23日，东北升，西北落；9月 23日至次年 3月 21日，东南升，西南落；3月 21日、9月 23日，正东升，正西落。
②正午前后太阳光的来向：判断太阳直射点与该点的方位。
（2）日影的长度L＝h×cotH。（h为物体高度，H为当时太阳高度），如图1所示。
Ⅱ．楼间距的问题：
北回归线以北地区建房时，为保证一楼全年均有阳光照到，两楼之间的最短距离与楼高的关系应满足 L≥h×cotH。（h为楼高，H为冬至日当地的正午太阳高度）。如图2所示。
Ⅲ．热水器的角度问题：
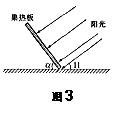
太阳能热水器的集热板要根据正午太阳高度的季节变化而调整角度，应满足α+H＝90°（α为集热板与地面之间的夹角，H为当天正午太阳高度）。如图3所示。