题目内容
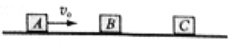
【题目】如图,三个质量相同的滑块A、B、C间隔相等地静置于同一水平直轨道上。现给滑块A向右的初速度v0,一段时间后A与B发生碰撞,碰后A,B分别以v0、v0的速度向右运动,B再与C发生碰撞,碰后B,C粘在一起向右运动。滑块A,B与轨道间的动摩擦因数为同一恒定值。两次碰撞时间均极短。求B,C碰后瞬间共同速度的大小。
【答案】![]() v0。
v0。
【解析】设滑块质量为m,A与B碰撞前A的速度为vA,由题意知,碰后A的速度vA’=![]() v0,B的速度vB’=
v0,B的速度vB’=![]() v0,由动量守恒定律得
v0,由动量守恒定律得
mvA= mvA’+ mvB
设碰撞前A克服轨道阻力所做的功为WA,由功能关系得
WA=![]() mv02-
mv02- ![]() mvA2
mvA2
设B与C碰撞前B的速度为vB’, B克服轨道阻力所做的功为WB,由功能关系得
WB=![]() mvB2-
mvB2- ![]() mvB’2
mvB’2
据题意可知,WA= WB,
设BC碰撞后瞬间共同速度的大小为v,由动量守恒定律得
mvB’= 2mv
联立解得:v=![]() v0。
v0。

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目