Question

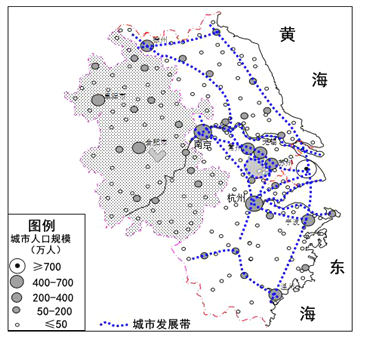
【题目】如图所示，假设在某个广场的某个灯柱上靠着一个醉鬼，他在灯柱周围随便走动，先朝一个方向走上几步，然后换个方向再迈上几步，如此这般，每走几步就随意折个方向。那么，他在这样弯弯折折地走了一段路程，比如折了100次以后，他离灯柱有多远呢？

Answer 1

【答案】10m

【解析】

我们用严格的数学方法来解答这个问题。

以广场上的灯柱为原点Ο建立坐标系，假设x轴指向南方，y轴指向东方，R表示醉鬼走过n个转折后（图中n为10）与灯柱的距离，实际上，醉鬼也不是按直线走路的，该图不是醉鬼实际运动的轨迹，若用和分别表示醉鬼所走路径的第n个分段在相应两轴上的投影 这里的x和y既有正数，又有负数，视这位醉鬼在各段具体路程中是离开还是接近灯柱而定，既然他的运动是完全无序的，因此在x和y的取值中，正数和负数的个数应该差不多。将上式第一项展开，有

②

这一长串数字包括了x的所有平方项和x的“混合积”，由于醉鬼走路是无规则的，他朝灯柱走和背着灯柱走的可能性相等，因此在x的各个取值中，正负会各占一半，这样，在那些“混合积”里，总是可以找出数值相等、符号相反的一对对可以互相抵消的数来，n的数目越大，这种抵消就越彻底。而平方项是正数，这样①式中的第1项就变成

。

X表示各段路程在x轴上投影长度的平均值（严格地说是方均根值）。同理，①式中第2项也能转化成，Y是各段路程在y轴上投影长度的平均值。这里利用了统计规律，考虑了由于运动的任意性所产生的可抵消的“混合积”。因此得到醉鬼离开灯柱的距离为

，即。

各路程的平均投影在两轴上是45°,所以就等于平均路程长度，用L来表示这个平均路程长度，可得。

即醉鬼在走了许多段不规则的弯路后，离灯柱的最可能距离为各段路程的平均长度乘以路径段数的平方根。因此，如果这个醉鬼每走lm就拐一个弯，那么在走了100m的长路后，他距灯柱的距离约为10m。