Question

【题目】如图所示，一个质量为M，半径为R的光滑均质半球，静置于光滑水平桌面上，在球顶有一个质量为m的质点，由静止开始沿球面下滑。试求：

（1）质点离开球面以前的轨迹；

（2）当质点m滑到方位角时（未脱离半球），质点的速度v的大小、方向怎样？质点相对半球的瞬时角速度为多少？

Answer 1

【答案】（1）质点的轨迹是一个长、短半轴分别为R和的椭圆。（2），，，。

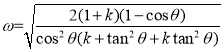【解析】

（1）为寻求轨迹方程，我们需要建立一个坐标：以半球球心O为原点，沿质点滑下一侧的水平轴为x坐标、竖直轴为y坐标。

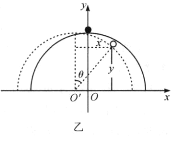
由于质点相对半球总是做圆周运动（离开球面前），有必要引入相对运动中半球球心的方位角来表达质点的瞬时位置，如图乙所示。

由水平方向的动量守恒，易得

,

即。 ①

而由图知：。 ②

不难看出，①、②两式实际上已经是一个轨迹的参数方程。为了明确轨迹的性质，我们可以将参数消掉，使它们成为

。

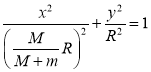这样，特征就明显了：质点的轨迹是一个长、短半轴分别为R和的椭圆。

（2）当质点滑至角位置时，设M的速度大小为v，质点m的水平速度与竖直速度分别为、，则，

。

又，角速度，

设，有，。

由上述各式可得

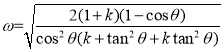，式中。