Question

【题目】一只钟，其分针长度是时针长度的两倍。问：午夜过后几点钟时分针的末端点和时针的末端点沿两端点的连线方向的分离速度最大？

Answer 1

【答案】11分钟

【解析】

解析：使用固定在分针上的转动参考系，则题目的解惊人得简单。在此参考系中，分针是静止的，而时针做“逆时针”转动。当时针末端速度的作用线通过分针的末端时，时针和分针离开的距离增加得最快。在这种情况下，时针臂、分针臂以及连其末端的直线构成一个直角三角形，如图所示。

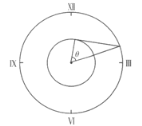
因为分针的长度是时针长度的两倍，其间的角度。

现在，我们可以计算午夜过后的什么时刻时针和分钟间的夹角为。因为分针转动的角速度是时针的12倍，故时针与12时之间的夹角可以由得出，即。因此，从12时算起，分针移动的角度为，时间恰好为午夜后11分钟。在后续时间里，时针与分针的夹角也会与上面相同（每小时两次），而第二次两针成此夹角时，分针与时针的末端将以最快的速度靠近。