题目内容
【题目】[选修4-1:几何证明选讲]如图,⊙O中 ![]() 的中点为P,弦PC,PD分别交AB于E,F两点.
的中点为P,弦PC,PD分别交AB于E,F两点.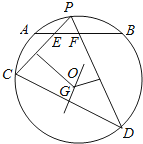
(1)若∠PFB=2∠PCD,求∠PCD的大小;
(2)若EC的垂直平分线与FD的垂直平分线交于点G,证明:OG⊥CD.
【答案】
(1)
解:连接PA,PB,BC,
设∠PEB=∠1,∠PCB=∠2,∠ABC=∠3,
∠PBA=∠4,∠PAB=∠5,
由⊙O中 ![]() 的中点为P,可得∠4=∠5,
的中点为P,可得∠4=∠5,
在△EBC中,∠1=∠2+∠3,
又∠D=∠3+∠4,∠2=∠5,
即有∠2=∠4,则∠D=∠1,
则四点E,C,D,F共圆,
可得∠EFD+∠PCD=180°,
由∠PFB=∠EFD=2∠PCD,
即有3∠PCD=180°,
可得∠PCD=60°
(2)
证明: 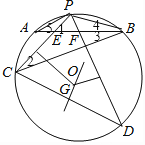 由C,D,E,F共圆,
由C,D,E,F共圆,
由EC的垂直平分线与FD的垂直平分线交于点G
可得G为圆心,即有GC=GD,
则G在CD的中垂线,又CD为圆G的弦,
则OG⊥CD.
【解析】(1)连接PA,PB,BC,设∠PEB=∠1,∠PCB=∠2,∠ABC=∠3,∠PBA=∠4,∠PAB=∠5,运用圆的性质和四点共圆的判断,可得E,C,D,F共圆,再由圆内接四边形的性质,即可得到所求∠PCD的度数;(2)运用圆的定义和E,C,D,F共圆,可得G为圆心,G在CD的中垂线上,即可得证.;本题考查圆内接四边形的性质和四点共圆的判断,以及圆的垂径定理的运用,考查推理能力,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目