题目内容
【题目】已知函数 ![]() (
( ![]() ,
, ![]() 为实数,
为实数, ![]() ,
, ![]() )
)
(1)若函数 ![]() 的图象过点
的图象过点 ![]() ,且方程
,且方程 ![]() 有且只有一个实根,求
有且只有一个实根,求 ![]() 的表达式;
的表达式;
(2)在(1)的条件下,当 ![]() 时,
时, ![]() 是单调函数,求实数
是单调函数,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:f(-2)=1得b=2a 且△=b2-4a=0 所以a=1,b=2 所以f(x)= x2+2x+1
(2)解:因为g(x)= x2+(2-k)x+1 所以 ![]()
![]() 2或
2或 ![]()
![]() -1 即k
-1 即k ![]() 6或k
6或k ![]() 0
0
所以k的取值范围 (-∞,0 ![]() ∪ [6,+∞)
∪ [6,+∞)
【解析】(1)由f(-2)=1,得b=2a,再结合f(x)=0方程只有一个根即判别式等于零分别求出a、b的值进而得出函数的解析式。(2)先根据已知整理 g(x) 的解析式,利用二次函数的图像和性质求得实数a的取值范围。
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】读我国东南某城镇农业布局图,下图四处发展棉花、果林、蔬菜和乳牛生产。
(1)请将上述农业适宜发展的农业类型填入表
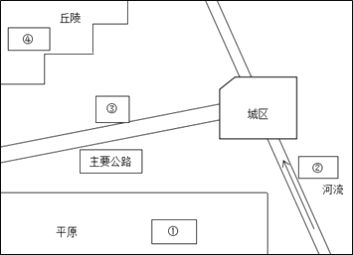
地区 | 农业类型 | 理由 |
① | ||
② | ||
③ |
(2)若④地农业开发利用不当,可能产生的生态环境问题是( )
A.草场退化 B.水土流失 C.生物多样性增加 D.环境污染