题目内容
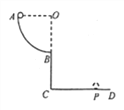
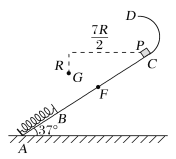
【题目】(2016全国卷Ⅰ，25)如图，一轻弹簧原长为2R，其一端固定在倾角为37°的固定直轨道AC的底端A处，另一端位于直轨道上B处，弹簧处于自然状态，直轨道与一半径为
R的光滑圆弧轨道相切于C点，AC＝7R，A、B、C、D均在同一竖直平面内。质量为m的小物块P自C点由静止开始下滑，最低到达E点(未画出)，随后P沿轨道被弹回，最高到达F点，AF＝4R，已知P与直轨道间的动摩擦因数μ＝
，重力加速度大小为g。(取sin 37°＝
，cos 37°＝
)
(1)求P第一次运动到B点时速度的大小；
(2)求P运动到E点时弹簧的弹性势能；
(3)改变物块P的质量，将P推至E点，从静止开始释放。已知P自圆弧轨道的最高点D处水平飞出后，恰好通过G点。G点在C点左下方，与C点水平相距
R、竖直相距R，求P运动到D点时速度的大小和改变后P的质量。
【答案】 (1)2
(2) 
mgR (3) 
m
【解析】 (1)由题意可知：lBC＝7R－2R＝5R①
设P到达B点时的速度为vB，由动能定理得
mglBCsin θ－μmglBCcos θ＝
mv②
式中θ＝37°，联立①②式并由题给条件得
vB＝2③
(2)设BE＝x，P到达E点时速度为零，此时弹簧的弹性势能为Ep，由B→E过程，根据动能定理得
mgxsin θ－μmgxcos θ－Ep＝0－mv④
E、F之间的距离l1为l1＝4R－2R＋x⑤
P到达E点后反弹，从E点运动到F点的过程中，由动能定理有
Ep－mgl1sin θ－μmgl1cos θ＝0⑥
联立③④⑤⑥式得
x＝R⑦
Ep＝mgR⑧
(3)设改变后P的质量为m1，D点与G点的水平距离为x1和竖直距离为y1，θ＝37°。由几何关系(如图所示)得：
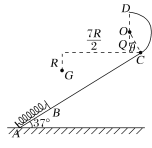
x1＝
R－
Rsin θ＝3R⑨
y1＝R＋R＋Rcos θ＝
R⑩
设P在D点的速度为vD，由D点运动到G点的时间为t。
由平抛运动公式得：
y1＝gt2
x1＝vDt
联立⑨⑩得
vD＝
设P在C点速度的大小为vC，在P由C运动到D的过程中机械能守恒，有
m1v＝m1v＋m1g(R＋cos θ)
P由E点运动到C点的过程中，由动能定理得
Ep－m1g(x＋5R)sin θ－μm1g(x＋5R)cos θ＝m1v
联立⑦⑧得
m1＝m
