题目内容
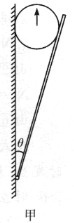
【题目】如图甲所示,有一木板可绕其下端的水平轴转动,转轴位于一竖直墙面上。开始时木板与墙面的夹角为![]() ,在夹角中放一正圆柱形木棍,截面半径为
,在夹角中放一正圆柱形木棍,截面半径为![]() 。在木板外侧加一力
。在木板外侧加一力![]() 使其保持平衡,在木棍端面上画一竖直向上的箭头。已知木棍与墙面之间、木棍与木板之间的静摩擦系数分别为
使其保持平衡,在木棍端面上画一竖直向上的箭头。已知木棍与墙面之间、木棍与木板之间的静摩擦系数分别为![]() ,
,![]() 。若极缓慢地减小所加的力
。若极缓慢地减小所加的力![]() ,使角慢慢张开,木棍下落。问:当夹角
,使角慢慢张开,木棍下落。问:当夹角![]() 张到
张到![]() 时,木棍端面上的箭头指向什么方向?
时,木棍端面上的箭头指向什么方向?
附三角函数表:
|
|
|
|
|
| 0.131 | 0.259 | 0.500 | 0.866 |
| 0.991 | 0.966 | 0.866 | 0.500 |
【答案】箭头最后指向为由正上方顺时针转![]() 处。
处。
【解析】
设木棍的质量为![]() ,所受墙面的正压力与摩擦力(向上)为
,所受墙面的正压力与摩擦力(向上)为![]() ;所受木板的正压力与摩擦力(向上)为
;所受木板的正压力与摩擦力(向上)为![]() 。设木板与墙面的夹角为
。设木板与墙面的夹角为![]() ,如图乙所示。则木棍的平衡方程为竖直方向
,如图乙所示。则木棍的平衡方程为竖直方向
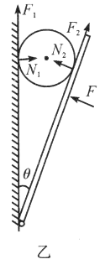
![]() . ①
. ①
水平方向:![]() . ②
. ②
转动:![]() . ③
. ③
1.要使木棍即将在墙面上先滑动(左滑),这时
![]() , ④
, ④
而![]() . ⑤
. ⑤
根据③式,左滑条件④⑤两式可合写为
![]() . ⑥
. ⑥
由②③④得
![]() . ⑦
. ⑦
由⑥⑦两式可得
![]() . ⑧
. ⑧
将![]() 代入⑧式,得
代入⑧式,得
![]() . ⑨
. ⑨
这就是左滑时![]() 所应满足的条件。
所应满足的条件。
由⑨式可以看出,当![]() 小时此式无法满足。可见左滑在
小时此式无法满足。可见左滑在![]() 大于临界角
大于临界角![]() 时发生,
时发生,![]() 满足
满足
![]() . ⑩
. ⑩
此式即⑧式取等号的情况,由此可知这时为同时处于最大摩擦力的临界状态。当![]() 小于
小于![]() 时发生右滑,即木棍在墙面上滑动而在木板上无滑动滚动。
时发生右滑,即木棍在墙面上滑动而在木板上无滑动滚动。
2.讨论木棍右滑条件,这时
![]() , ④
, ④![]()
![]() . ⑤
. ⑤![]()
右滑条件成为![]() . ⑥
. ⑥![]()
由②③④![]() 式得
式得![]() 与
与![]() 的关系为
的关系为
![]() . ⑦
. ⑦![]()
由⑥![]() ⑦
⑦![]() 式得
式得
![]() . ⑧
. ⑧![]()
此式正好与⑧式相反,即右滑在![]() 小于⑩式的
小于⑩式的![]() 时发生。结论:当
时发生。结论:当![]() 时右滑,即在木板上滑动;当
时右滑,即在木板上滑动;当![]() 时左滑,即在墙面上滑动。
时左滑,即在墙面上滑动。
3.求临界角![]() ,即解⑩式.
,即解⑩式.
两边平方并消去![]() 得
得
![]() .
.
其解为 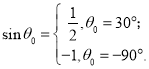
![]() 满足⑩式,是所求的解;而另一解
满足⑩式,是所求的解;而另一解![]() 不满足⑩式,是增根,应舍去。结果:当
不满足⑩式,是增根,应舍去。结果:当![]() 时右滑(在木板上滑动);当
时右滑(在木板上滑动);当![]() 时左滑(在墙面上滑动).
时左滑(在墙面上滑动).
4.计算箭头转角
设张角在![]() ,
,![]() ,
,![]() 时木棍中心的高度(从转轴算起)分别为
时木棍中心的高度(从转轴算起)分别为![]() .
.
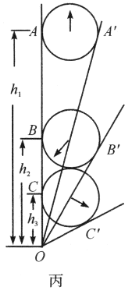
由于![]() ,由图丙可知
,由图丙可知
![]() ,
,
![]() ,
,
![]() .
.
当木棍由![]() 下落至
下落至![]() 时,顺指针转
时,顺指针转![]() 角:
角:
![]() .
.
当木棍由![]() 下落至
下落至![]() 时,逆时针转
时,逆时针转![]() 角:
角:
![]() .
.
而在这一过程中,木板本身顺指针转了![]() ,因此箭头的最后指向为
,因此箭头的最后指向为![]() 。所以,箭头最后指向为由正上方顺时针转
。所以,箭头最后指向为由正上方顺时针转![]() 处。
处。

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案