Question

【题目】如图所示，在xOy平面上有两个半径均为R的圆，左圆圆心固定在坐标原点O，右圆圆心沿x轴以速度做匀速直线运动，时刻两圆心重合。试求两圆交点之一P点的速率v及向心加速度与时间t的关系。

Answer 1

【答案】 ；

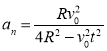
【解析】

由图可知,任意时刻P点的x轴坐标与点坐标的关系为。

则P点速度的水平分量一定有。

可见,交点P在x方向做匀速运动。

又由于在圆环O上运动,其运动方向一定是沿圆环的切线方向的,由图乙可知,P点的速度v与间有如下关系:

，式中。

而，，且，

由此可得。

因P绕左圆环做圆周运动,故其向心加速度为

。

当然,P绕右圆环也是做圆周运动的,由对称性易知,P绕右圆环运动的向心加速度亦为。

解题时,若能通过定性分析得到结果,哪怕是部分结论,都会比定量分析来得迅捷,同时也会为后续的计算带来便利,如本题中对P点x方向上的速度的分析,这种一举多得的方法,是值得我们认真学习与效仿的。