题目内容
【题目】阅读下列图文资料,回答问题。
某校地理研究性学习小组同学通过测量学校旗杆影子长度的变化,探究正午太阳高度的变化特点,并绘制了示意图(图1),其中OAB为地平面,PE 为太阳光线, AEB所在弧为杆影端点轨迹。

(1)图1中能指示当地经线的线段是 ,地方时正午时刻的旗杆影长是 ,其长度为一天中 。若旗杆的长度为L,用函数式表示当天正午太阳高度H的大小。
(2)图1中,若地平面上α与β角度相等,用地理语言表述旗杆影子端点A、B分别出现的两个时刻有何关系?
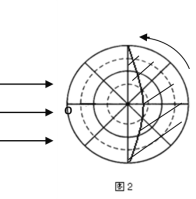
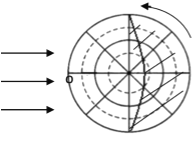
(3)今年北京时间6月19日12时18分,该小组同学发现旗杆在阳光下瞬间失去黑影,出现“立竿无影”的现象,由此可知,该现象年内可能出现 次,该校所在地的经度是 ,在图2中绘制此时太阳照射地球示意图(画出晨昏线、用阴影表示黑夜,用箭头标出地球自转方向和太阳光线)
(4)若冬至日测得正午旗杆影长为OEˊ,推导该学校地理纬度φ的计算公式
【答案】(1)OE OE 最短 H=arc cot(OE / L )
(2)两时刻与杆影最短时即当地地方时12时的时差相等
(3)两 东经115.5° 作图(如下)
(4)当地纬度:φ=90°— 23°26′—arc cot(OEˊ/ L ) =66°34′—arc cot(OEˊ/ L)
【解析】
本题主要考查正午太阳高度及日影等问题,试题难度较难。
(1)据所学知识可知,经线指示的是南北方向,符合的是OE;一天中,正午时太阳高度最高,影长最短,符合的是OE;若旗杆的长度为L,当天正午太阳高度H=arc cot(OE/L)。
(2)据所学知识可知,若地平面上α与β角度相等,说明旗杆影子到端点A的时间与正午12时的时间间隔和旗杆影子到端点B的时间与12时的时间间隔相等;也就是两时刻与杆影最短时即当地地方时12时的时差相等。
(3)北京时间6月19日12时18分,该小组同学发现旗杆在阳光下瞬间失去黑影,出现“立竿无影”的现象,可以判断该地被太阳直射,此时太阳直射点位于赤道与北回归线之间,一年有两次太阳直射;北京时间12时18分时,当地时间为12:00,两地相差18分钟,经度相差4.5°,可计算出当地的经度为115.5°E。此时太阳照射地球示意图如下:
(4)若冬至日测得正午旗杆影长为OE′,根据旗杆的长度为L,可计算出冬至日正午太阳高度为arc cot(OE′/L)=90°—(23°26′+φ),所以当地纬度φ= 90°—23°26′—arc cot(OE′/L)=66°34′—arc cot(OE′/L)。