Question

【题目】长l的均匀细棒，质量线密度为λ，开始时一端温度为，另一端温度为，中间各处温度线性地分布，此棒在绝热的情况下，最终达到热平衡。已知棒各处的比热为相同的常量C。试求全过程棒的熵增量，并说明此过程是否可逆。

Answer 1

【答案】。棒的总熵增量,这是不可逆过程。

【解析】

棒的初始温度分布容易求得。因过程绝热，棒与外界无热量交换，只是棒中温度较低处从温度较高处吸热而升温，同时温度较高处向温度较低处放热而降温，最后棒各处达到一致的温度。由棒吸热与放热总量平衡，可确定全棒的温度。棒中各小段从其初温达到终温，相应有熵的增量，各小段熵增量之和即为全过程棒的熵增量。由棒的熵增量的正、负号，即可确定过程是否可逆。

其实，这一过程就是热量自发地从高温物体向低温物体传输的过程。由热力学第二定律可知，这是一个不可逆过程，因此全过程的熵增量必定为正。解答过程如下：沿棒取x坐标如图所示。

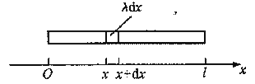
据图有，。

因棒各处温度线性地分布，故棒中任意x处的温度为。

设在绝热条件下达到热平衡后，棒各处的温度同为，则从x到（）小段的吸热量应为。

因是绝热的，棒的吸热Q应为零，对上式积分，可得

，即。

棒中从x到（）小段，在全过程中，温度从初态的达到终态的。该小段在任意元过程中，温度从Τ增为（）时的熵增量为。

该小段从初态达到终态的熵增量为。

各小段在全过程中的熵增量之和即为棒在全过程中总熵增量△S,应为。

把和的表达式代入，得。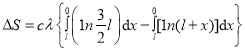

利用积分公式：，

最后可得。

可见，在全过程中，棒的总熵增量,为正，因此，这是不可逆过程。