题目内容
【题目】)
硬质长方形薄塑料绝缘板长为2![]() l(垂直纸面向里的长度)、宽为
l(垂直纸面向里的长度)、宽为![]() l(如图),共有2n块,与水平面成45°角按图所示放置,最左边的称为第一块,依次往右第二块、第三块……。PQ间的整个空间有水平向右的匀强磁场,同时在PQ间加上电压U(P的电势高于Q的电势,PQ间区域足够宽广),在O点正对塑料板的正中央处从静止释放一个质子(电荷量为e,质量为m),质子与板的碰撞没有动能的损失,并且碰撞后电压消失,接着碰撞后又恢复,如此反复。(sin 37°=0.6,cos 37°=0.8)试求:
l(如图),共有2n块,与水平面成45°角按图所示放置,最左边的称为第一块,依次往右第二块、第三块……。PQ间的整个空间有水平向右的匀强磁场,同时在PQ间加上电压U(P的电势高于Q的电势,PQ间区域足够宽广),在O点正对塑料板的正中央处从静止释放一个质子(电荷量为e,质量为m),质子与板的碰撞没有动能的损失,并且碰撞后电压消失,接着碰撞后又恢复,如此反复。(sin 37°=0.6,cos 37°=0.8)试求:

(1)质子与第一块板碰撞时的速度多大?
(2)为使质子能打在Q板上(正对O点的地方O′点),磁感应强度的最大值B为多少?
(3)在满足(2)的条件下,质子从出发到打在Q上经历了多长的时间?
(4)如果当第一次碰完第2n-1块时,塑料板全部脱落电压也依然存在,在满足(2)的前提下,质子将打在Q板何处?(以O′为坐标原点,竖直向上为y轴正向,垂直向外为x轴正向,用坐标点表示,计算中取![]() ,
, ![]() )
)
【答案】(1) ![]() (2)
(2) ![]() (3) t=2nl(
(3) t=2nl(![]() +
+![]() )
)![]() (4) (-1.8l
(4) (-1.8l![]() ,0.6l
,0.6l![]() )
)
【解析】试题分析:先求出板间的距离,再跟据场强公式得出场强,由动能定理求出质子与第一块板碰撞时的速度为v1;根据洛伦兹力提供向心力,得出半径表达式,当半径最小时时,磁感应强度有最大值;粒子在板间运动的时间包括直线运动时间和做圆周运动的时间,根据运动学公式和粒子的周期公式即可解题;最后还余下的长度为1.5l,质子反弹后方向竖直向上,因此竖直面内匀速圆周运动,水平方向做初速度为零的匀加速运动,根据半径与距离的关系求出打的位置。
(1)PQ两板间的距离为: ![]()
板间的电场强度为: ![]()
质子与第一块板碰撞时的速度为v1,
根据动能定理得: ![]()
解得: ![]()
(2)由题意可知最小半径为: ![]()
根据洛伦兹力提供向心力: ![]()
解得: ![]()
以上联立解得: ![]()
(3)令粒子直线运动的时间t1,根据牛顿第二定律: ![]()
联立以上解得![]()
粒子运动的距离为: ![]()
联立解得: ![]()
粒子做圆运动的时间t2:
粒子运动的周期为: ![]()
粒子做圆运动的总时间为: ![]()
粒子运动的总时间为: ![]()
(4)最后还余下的长度为1.5l,质子反弹后方向竖直向上,因此竖直面内匀速圆周运动,水平方向做初速度为零的匀加速运动。
由位移时间关系: ![]()
联立以上解得: ![]()
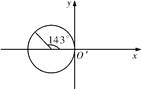
而周期: ![]()
所以粒子运动了143°,如图所示。
粒子碰该板的速度为: ![]()
此时离子半径为半径: ![]()
沿X方向的距离为: ![]()
沿X方向的距离为: ![]()
则: ![]()