题目内容
【题目】一载有电流
的导线弯成椭圆形，椭圆的方程为
，
，如图所示，试求在椭圆中心
产生的磁感强度
【答案】
【解析】
根据毕奥-萨伐尔定律，椭圆上的电流元
在椭圆中心
产生的磁感强度为
， ①
式中
是电流元到的矢量，有
， ②
式中
为垂直于纸面向外的单位矢量，由图乙可见
． ③
将式②③代入式①便得
． ④
为了积分，换成用极坐标表示，以椭圆中心为极点，
轴为极轴，如图所示，便有
，
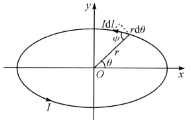
． ⑤
代入椭圆方程得
， ⑥
得出
． ⑦
代入式④得所求的磁感强度为
． ⑧
这个积分是一种椭圆积分，为了化成标准形式，作如下变换：
． ⑨
所以，
． ⑩
代入式⑧，并由
是
的以
为周期的函数，便得
，
式中，
是椭圆的离心率，
．
式中的积分叫作第二类全椭圆积分，其值为
于是得所求的磁感强度为
．
本题从练习功能上讲，与上题有相似之处，特别是在积分技巧方面，肯定是需要中学生特别注意并加以训练的．
既然竞赛不再回避积分运算，那么二次函数的积分一定是竞赛生需要掌握的内容，希望本章中的相关练习题对读者有所帮助．
练习册系列答案
轻松暑假总复习系列答案
相关题目
