题目内容
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
【答案】
(1)解:当a=2时,f(x)≥4﹣|x﹣4|可化为|x﹣2|+|x﹣4|≥4,
当x≤2时,得﹣2x+6≥4,解得x≤1;
当2<x<4时,得2≥4,无解;
当x≥4时,得2x﹣6≥4,解得x≥5;
故不等式的解集为{x|x≥5或x≤1}
(2)解:设h(x)=f(2x+a)﹣2f(x),则h(x)= 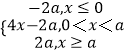
由|h(x)|≤2得 ![]() ,
,
又已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},
所以 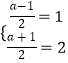 ,
,
故a=3.
【解析】(1)当a=2时,f(x)≥4﹣|x﹣4|可化为|x﹣2|+|x﹣4|≥4,直接求出不等式|x﹣2|+|x﹣4|≥4的解集即可.(2)设h(x)=f(2x+a)﹣2f(x),则h(x)= 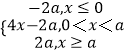 .由|h(x)|≤2解得
.由|h(x)|≤2解得 ![]() ,它与1≤x≤2等价,然后求出a的值.
,它与1≤x≤2等价,然后求出a的值.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目