Question

【题目】
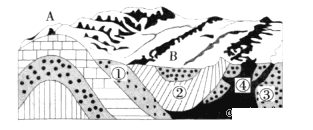
如图，O为等腰三角形ABC内一点，圆O与ABC的底边BC交于M、N两点与底边上的高AD交于点G，与AB、AC分别相切于E、F两点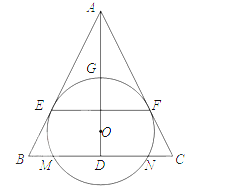

（1）（Ⅰ）证明：EF||BC
（2）（Ⅱ）若AG等于圆O的半径，且AE=MN=2，求四边形EBCF的面积

Answer 1

【答案】
（1）

见解答

（2）

【解析】（I）由于ABC是等腰三角形，ADBC，所以AD是CAB的平分线，又因为圆O分别与AB、AC相切于E、F两点，所以AE=AF，故ADEF,从而EF//BC。
(II)由（I）知，AE=AF，ADEF，故AD是EF的垂直平分线，又EF是圆O的弦，所以O在AD上，连接OE,OM，则OEAE。由AG等于圆O的半径得AO=2OE,所以OAE=30，所以ABC和AEF都是等边三角形，因为AE=2，所以AO=4，OE=2
因为OM=OE=2，DM=MN=，所以OD=1，于是AD=5，AB=，所以四边形EBCF的面积X（）2X-X（2）2X=