题目内容
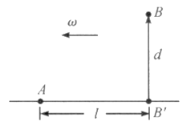
【题目】河岸边有人A,他可以在岸上以速度υ奔跑,也可以在水中以速度u(相对水)游泳,水流速为![]() ,如图所示。离岸d处有浮筒B(用锚链固定在河底上),开始
,如图所示。离岸d处有浮筒B(用锚链固定在河底上),开始![]() 。问:此人应在何处下水,才能使他到达B的时间最短?
。问:此人应在何处下水,才能使他到达B的时间最短?
【答案】A的上游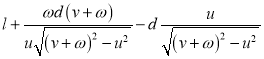 处下水
处下水
【解析】
选择流水为参照,浮筒以ω的速度向右运动,人在岸上跑的速度为![]() ,人在水中游的速度为u.根据折射定律有(θ为折射角)
,人在水中游的速度为u.根据折射定律有(θ为折射角)![]() 。
。
人在岸上走的路程为(行走时间为![]() )
)![]() 。
。
人总共沿岸方向的位移为
![]() 。
。
在垂直于河岸方向上有![]() 。
。
由以上两式消去![]() ,可得
,可得
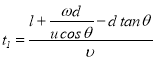 。
。
人相对岸走的路程为
![]() 。
。
将折射定律代入可得
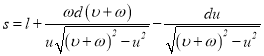 。
。
解答物体在两个不同的速度区域运动时的时间极值问题,多将光的传播所遵循的折射定律或者费马原理迁移至此,讨论运动物体到达某确定点的时间最小值,或者是在一定时间内所能到达的区域.这一情况,我们在《高中物理竞赛辅导教程(新大纲版)》中已有示例。
本题的特别之处在于水是流动的,由此,人在不同区域内运动的速度就变得复杂起来.而当选择流水为参照时,首先是折射定律的表述有所变化,其次是目标点(浮筒)在运动,几何关系也复杂起来,稍有差池,便会导致出错。
解答此题的关键是要选择流水为参照。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目