Question

【题目】光滑的水平地面O上有一质量为M的滑块，滑块表面上有一质量可忽略的钉子O，O处系着长为l的轻绳，绳下系着质量为m的小球．开始时系统处于静止状态，如图甲所示，轻绳与竖直甲方向有一很小的夹角，而后让小球自由摆下，形成往返运动．设小球摆动过程中不会与滑块表面接触，也不会与地面接触，且滑块不会倾倒，试求小球的摆动周期．

Answer 1

【答案】

【解析】

先讨论摆线长为l、幅角也为的单摆．设摆球质量为，则在的小过程中摆球的运动速度可由能量方程

求得，为．

该摆的周期为．

再讨论题设摆的运动．摆球首先朝左方摆动，同时滑板因系统水平方向动量守恒而朝右运动。摆线到达左侧与竖直线之间达夹角时，系统又处于静止状态．而后摆球将朝右方摆动，滑板朝左运动，再次回到初始状态，完成系统的一次周期运动．这一周期运动中，摆球相对滑板做一次幅角为的类单摆运动

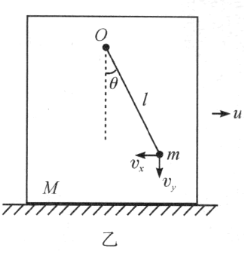
如图乙所示，摆角为时摆球相对地面的水平、竖直分速度记为、，滑板的水平反向运动速度记为u，则据能量守恒有．

水平方向动量守恒关系为．

摆球相对滑板做圆运动，如图丙所示，有运动关联

．

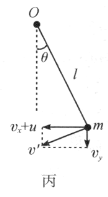
图中为摆球相对滑板的运动速率．由上述三式可得

．

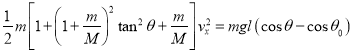为小量，可略，可得

，

．

参考图示，可得．为小量，近似取1，有

．

于是，任意一对小过程的速度间均有确定的比例关系

各自对应的时间为，．

一对小过程所经时间均有确定的比例关系

全过程经历时间T与之间的比例关系便为．

于是有．