题目内容
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 时,若函数
时,若函数![]() 有三个不同的零点,求
有三个不同的零点,求![]() 的取值范围;
的取值范围;
(3)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,请你探究当
的“类对称点”,请你探究当![]() 时,函数
时,函数![]() 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
【答案】(1) ![]() 和
和![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】试题分析:(1)由f′(x)="2x-(a+2)+" ![]() =
=![]() =
=![]()
,能求出当a>2时,求函数f(x)的单调递增区间.
(2)a=4,f′(x)=2x+![]() -6,故f′(x)="2x+"
-6,故f′(x)="2x+"![]() -6≥4
-6≥4![]() -6,不存在6x+y+m=0这类直线的切线.
-6,不存在6x+y+m=0这类直线的切线.
(3)y=g(x)=(2x0+![]() -6)(x-x0)+
-6)(x-x0)+ ![]() -6x0+4lnx0,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.
-6x0+4lnx0,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.
解:(1)由![]() 可知,函数的定义域为
可知,函数的定义域为![]() ,
,
且![]() .
.
因为![]() ,所以
,所以![]() .
.
当![]() 或
或![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)当![]() 时,
时, ![]() .
.
所以,当![]() 变化时,
变化时,![]() ,
, ![]() 的变化情况如下:
的变化情况如下:
| (0,1) | 1 | (1,2) | 2 | (2, |
| + | 0 | — | 0 | + |
| 单调递增 |
| 单调递减 |
| 单调递增 |
所以![]() ,
,
![]() .
.
函数![]() 的图象大致如下:
的图象大致如下:
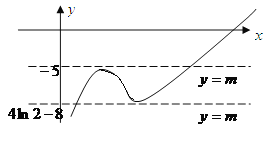
所以若函数![]() 有三个不同的零点,
有三个不同的零点, ![]() .
.
(3)由题意,当![]() 时,
时, ![]() ,则在点P处切线的斜率
,则在点P处切线的斜率![]()
![]() ;所以
;所以
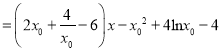 .
.
令 ,
,
则![]() ,
,  .
.
当![]() 时,
时, ![]() 在
在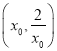 上单调递减,所以当
上单调递减,所以当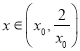 时,
时, ![]() 从而有
从而有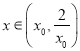 时,
时,![]() ;
;
当![]() 时,
时, ![]() 在
在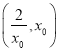 上单调递减,所以当
上单调递减,所以当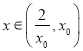 时,
时, ![]() 从而有
从而有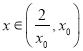 时,
时, ![]() ;所以在
;所以在![]() 上不存在“类对称点”.
上不存在“类对称点”.
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上是增函数,故
上是增函数,故![]()
所以![]() 是一个类对称点的横坐标.
是一个类对称点的横坐标.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目