题目内容
【题目】房地产开发商在某城市(31.5°N)计划建造两栋商品住宅楼,为使北楼所有朝南房屋在正午时终年都能被太阳照射,在两栋楼水平间距为40米的情况下,南楼的高度最高约为多少米?(可能会用到的数据:tan35°≈0.7,tan45°≈1,tan60°≈1.8tan82°≈7.1)
过程:该城市的楼房会在冬至日达到正午太阳高度的最小值,即冬至日时楼房的影子最长,最容易遮挡住北楼的阳光,该城市冬至日的正午太阳高度为:H=90°﹣纬度差(太阳直射点纬度和当地纬度的差值)=90°﹣(31.5°N+23.5°S)=35°设南楼高度为X米,则根据几何知识可得:tan35°=X/40米解得:X=28米;结论:南楼的高度最高约为米.
【答案】28
【解析】如下图所示,只要算出冬至日该地的正午太阳高度就可以求出南楼的高度.
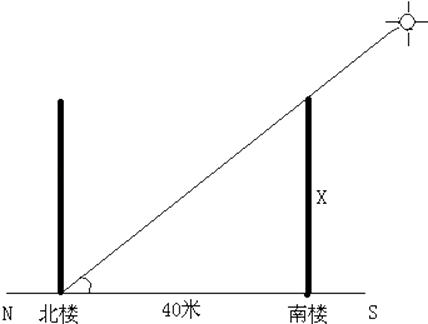
所以答案是:过程:该城市的楼房会在冬至日达到正午太阳高度的最小值,即冬至日时楼房的影子最长,最容易遮挡住北楼的阳光,该城市冬至日的正午太阳高度为:H=90°﹣纬度差(太阳直射点纬度和当地纬度的差值)=90°﹣(31.5°N+23.5°S)=35°设南楼高度为X米,则根据几何知识可得:tan35°=X/40米;解得:X=28米;结论:南楼的高度最高约为28米.

练习册系列答案
相关题目




