题目内容
【题目】已知圆C的圆心与点P(﹣2,1)关于直线y=x+1对称,直线3x+4y﹣11=0与圆C相交于A,B点,且|AB|=6,则圆C的方程为( )
A.x2+(y+1)2=18
B.(x+1)2+y2=9
C.(x+1)2+y2=18
D.x2+(y+1)2=9
【答案】A
【解析】解:根据题意,设圆C的圆心C(a,b),半径为r,则其标准方程为:(x﹣a)2+(y﹣b)2=r2,
圆C的圆心与点P(﹣2,1)关于直线y=x+1对称,
必有 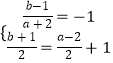 ,解可得
,解可得 ![]() ,
,
圆心C到直线3x+4y﹣11=0的距离d= ![]() =3
=3
又由直线3x+4y﹣11=0与圆C相交于A,B点,且|AB|=6,
则其半径r2=32+32=18,
故其标准方程为:x2+(y+1)2=18,
所以答案是:A.
【考点精析】关于本题考查的直线与圆的三种位置关系,需要了解直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能得出正确答案.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目






