题目内容
【题目】一宇宙人在太空(万有引力可以忽略)玩垒球,辽阔的太空球场半侧存在均匀电场E,另半侧存在均匀磁场B,电场与磁场的分界面为平面,电场方向与界面垂直,磁场方向垂直纸面指向里。宇宙人位于电场一侧距界面为h的P点,O点是P点至界面垂线的垂足,D点位于纸面上O点的右侧,OD与磁场B的方向垂直,![]() ,如图所示。垒球的质量为m,且带有电量
,如图所示。垒球的质量为m,且带有电量![]() 。
。

(1)宇宙人是否可能自P点以某个适当的投掷角(与界面所成的夹角)![]() 及适当的初速度
及适当的初速度![]() 投出垒球,使它经过D点,然后历经磁场一次自行回至P点?试讨论实现这一游戏,d必须满足的条件并求出相应
投出垒球,使它经过D点,然后历经磁场一次自行回至P点?试讨论实现这一游戏,d必须满足的条件并求出相应![]() 、
、![]() 。
。
(2)若宇宙人从P点以初速度![]() 平行于界面投出垒球,要使垒球击中界面上的某一D点,初速度
平行于界面投出垒球,要使垒球击中界面上的某一D点,初速度![]() 的指向和大小应如何?
的指向和大小应如何?
【答案】(1)![]()
![]() ,
,![]() ;
;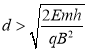
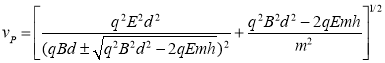 ,
,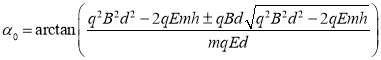 (2)见解析
(2)见解析
【解析】
(1)(ⅰ)如图1所示,以O为原点,作一直角坐标系,使x轴与直线OD重合,y轴与直线OP重合。根据题中所给条件,若宇宙人在![]() 面内将垒球投向y轴的右侧,使垒球保持在
面内将垒球投向y轴的右侧,使垒球保持在![]() 平面内运动,则在电场区,垒球做斜抛(或平抛)运动,当垒球到达分界面上的D点时,其速度
平面内运动,则在电场区,垒球做斜抛(或平抛)运动,当垒球到达分界面上的D点时,其速度![]() 与x轴夹角为
与x轴夹角为![]() 。进入磁场区后,垒球沿半径为R的圆弧运动,到达界面的另一点
。进入磁场区后,垒球沿半径为R的圆弧运动,到达界面的另一点![]() ,又从
,又从![]() 进入电场区做斜上抛运动。只要
进入电场区做斜上抛运动。只要![]() 位于x轴上O点的左侧,且
位于x轴上O点的左侧,且![]() ,垒球就能自
,垒球就能自![]() 斜抛恰好回到P点。
斜抛恰好回到P点。
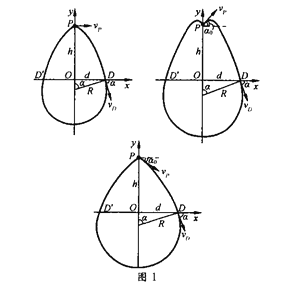
由于![]() , ①
, ①
因而![]() 。
。
设a为垒球在电场区垂直“下落”的加速度,得
![]() , ②
, ②
所以![]()
![]() , ③
, ③
式中“+”与“-”分别对应于在P点做斜上抛与斜下抛的情况。
设垒球从P点到D点所经历的时间为![]() ,则
,则
![]() , ④
, ④
而![]() , ⑤
, ⑤
将②⑤式代入④式,得![]() ,
,
解得![]()
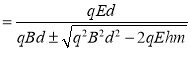 。 ⑥
。 ⑥
因③式和⑥式是实数,故必须满足条件:
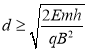 。
。
①若![]() ,
,
则由③式和⑥式可得![]() ,
,![]() ,
,
即![]() ,
,![]() 。
。
②若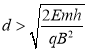 ,
,
则有![]()
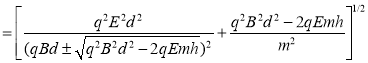 ,
,
![]()
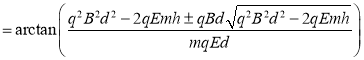 。
。
式中根式前面取“+”号对应于从P点做斜向上抛的运动,取“-”对应于从P点做斜向下抛的运动(如图1所示)。
③当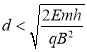 时,无论怎样选取
时,无论怎样选取![]() 和
和![]() ,投出的垒球都无法按题中要求回至P点。
,投出的垒球都无法按题中要求回至P点。
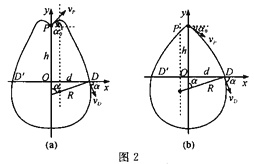
(ⅱ)在![]() 与D并不关于O点对称的情况下,垒球亦有可能回到抛出点,此时,垒球在电场区域内的运动构成一段完整的抛物线,如图2所示。
与D并不关于O点对称的情况下,垒球亦有可能回到抛出点,此时,垒球在电场区域内的运动构成一段完整的抛物线,如图2所示。
仍将![]() 分解为
分解为![]() 与
与![]() ,在磁场区域,由前面的解答易得
,在磁场区域,由前面的解答易得![]() 。
。
在电场区域,有
![]() ,
,![]() 。
。
由此易知![]() 。
。
先考虑如图2(a)所示的情形,此时垒球斜向上抛,此情形下,垒球从P点运动到D点,所用时间为![]() ,
,
解得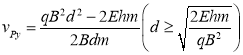 ,
,
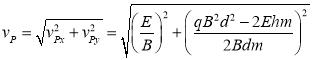 ,
,
![]() 。
。
再考虑如图2(b)所示的情形,此时垒球斜向下抛,同理可得
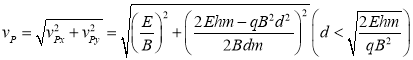 ,
,
![]() 。
。
(2)平行于界面的初速度![]() 必须指向正x轴方向才有可能击中D点。击中D点方式有如下三种:
必须指向正x轴方向才有可能击中D点。击中D点方式有如下三种:
①从P点平抛出后经过电场区域,直接到达D点。若所经历时间为t,则由
![]() ,
,![]()
消去t,得![]() 。
。
②从P点向右平抛“下落”,然后经磁场回转,又在电场区斜上抛,如此循环,历经磁场n次,最终在电场区经斜上抛到达D点,如图3(a)所示。
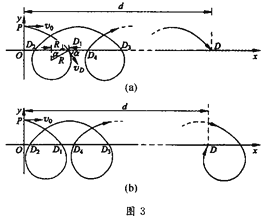
设自P点平抛的水平射程![]() 。垒球经磁场回转一次,在x轴方向倒退
。垒球经磁场回转一次,在x轴方向倒退![]() 。其中
。其中
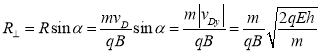 。
。
从![]() 出磁场区后经电场区的斜上抛运动,垒球在x轴方向前进
出磁场区后经电场区的斜上抛运动,垒球在x轴方向前进![]() 。如此历经n次循环,最后从电场区到达D点,应有
。如此历经n次循环,最后从电场区到达D点,应有
![]() ,
,
解得![]() 。
。
若P点抛出的初速度为![]() ,则由
,则由
![]() ,
,![]()
消去t,得![]() ,或
,或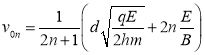 。
。
③自P点向右平抛“下落”,再经磁场回转,然后在电场区斜上抛,如此循环,历经磁场n次,最终在磁场区回转到达D点,如图3(b)所示。
设自P点平抛的水平射程为![]() ,则应有
,则应有
![]() ,
,
解得![]() 。
。
相应的初速度为![]() ,则有
,则有
![]() ,
,
或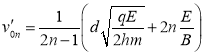 ,
,
以上各式中n=1,2,3,…。