题目内容
【题目】已知f(x)=|2x+3|﹣|2x﹣1|.
(Ⅰ)求不等式f(x)<2的解集;
(Ⅱ)若存在x∈R,使得f(x)>|3a﹣2|成立,求实数a的取值范围.
【答案】解:(Ⅰ)不等式f(x)<2,
等价于 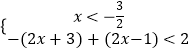 或
或 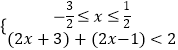 或
或 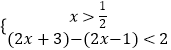 ,
,
得 ![]() 或
或 ![]() ,
,
即f(x)<2的解集是(﹣∞,0);
(Ⅱ)∵f(x)≤|(2x+3)﹣(2x﹣1)|=4,
∴f(x)max=4,∴|3a﹣2|<4,
解得实数a的取值范围是 ![]() .
.
【解析】1.根据f(x)画出分段函数图像;2.根据第一问要求写出对应的分段函数式,注意讨论及取值;3.注意“f(x)>|3a﹣2|成立”隐藏的关系,即|3a﹣2|比f(x)max都要小时的实数a的取值范围。
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目