题目内容
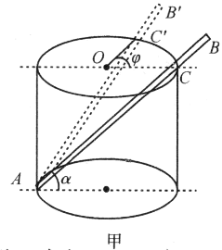
【题目】如图甲所示,杆![]() 放在圆筒内,杆的
放在圆筒内,杆的![]() 端用铰链固定在筒壁与筒底的交界处,杆的
端用铰链固定在筒壁与筒底的交界处,杆的![]() 点靠在筒的边缘上。
点靠在筒的边缘上。![]() 两点位于通过圆筒轴的竖直平面内,杆与水平线所成的角度为
两点位于通过圆筒轴的竖直平面内,杆与水平线所成的角度为![]() 。使杆沿筒的边缘移动到
。使杆沿筒的边缘移动到![]() 点,
点,![]() 为
为![]() 。试问:摩擦系数最小为多少,杆在
。试问:摩擦系数最小为多少,杆在![]() 位置能保持平衡?
位置能保持平衡?
【答案】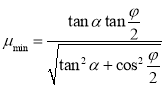
【解析】
方法1 作用在杆上的力有:重力、![]() 点处铰链的支持力、
点处铰链的支持力、![]() 点处的圆筒的支持力
点处的圆筒的支持力![]() 和摩擦力
和摩擦力![]() 。杆平衡的条件是这些力的合力为零以及力矩的代数和为零。对于通过
。杆平衡的条件是这些力的合力为零以及力矩的代数和为零。对于通过![]() 点竖直轴,铰链的支持力力矩和杆重力力矩都为零,则力
点竖直轴,铰链的支持力力矩和杆重力力矩都为零,则力![]() 和
和![]() 的合力一定通过杆的竖直平面。我们分析合力的水平分量,确定
的合力一定通过杆的竖直平面。我们分析合力的水平分量,确定![]() 和
和![]() 的方向以及它们在水平面的投影值——
的方向以及它们在水平面的投影值——![]() 和
和![]() ,坐标轴
,坐标轴![]() 分别为从
分别为从![]() 点指向圆心、圆的切线方向和竖直向上的方向上(如图乙所示).
点指向圆心、圆的切线方向和竖直向上的方向上(如图乙所示).
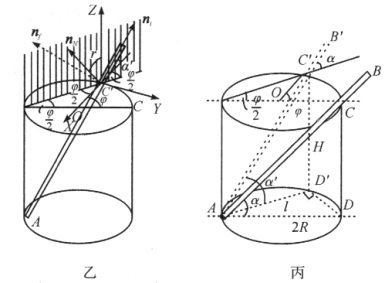
我们引入三个单位矢量![]() ,其方向分别沿杆、力
,其方向分别沿杆、力![]() 和力
和力![]() 。设
。设![]() 与水平线成角
与水平线成角![]() 。由于杆转动,杆所在竖直平面转动角
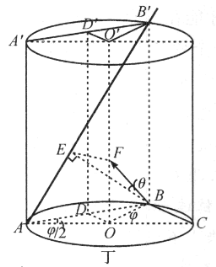
。由于杆转动,杆所在竖直平面转动角![]() 。在图丙中,
。在图丙中,![]() 表示筒高,
表示筒高,![]() 表示圆筒的半径。在
表示圆筒的半径。在![]() 中,
中,![]() ;在
;在![]() 中,
中,![]() 。在
。在![]() 中,
中,![]() .
.
因而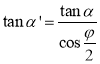 .
.
用单位矢量![]() 和
和![]() 来表示
来表示![]() .
.
![]() .
.
力![]() 垂直于杆并且与圆相切于
垂直于杆并且与圆相切于![]() 点,由此可知,矢量
点,由此可知,矢量![]() 垂直于矢量
垂直于矢量![]() 和矢量
和矢量![]() ,即
,即
![]() . ①
. ①
由此得到角![]() 和
和![]() 之间的关系为
之间的关系为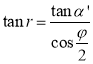 .
.
为了确定矢量![]() 的方向,考虑到它也垂直于矢量
的方向,考虑到它也垂直于矢量![]() 和矢量
和矢量![]() ,经不太复杂的计算得到
,经不太复杂的计算得到
![]() ②
②
由①和②可以得到![]() ,
,![]() ;
;
![]() ,
,
![]() .
.
正如已指出的那样,力![]() 和力
和力![]() 的合力在水平方向投影应位于杆的铅直平面内,即
的合力在水平方向投影应位于杆的铅直平面内,即
![]() .
.
摩擦系数的最小值![]() 由关系式
由关系式![]() 确定,于是
确定,于是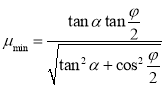 .
.
方法2 支持力![]() 应垂直于过
应垂直于过![]() 点且与圆
点且与圆![]() 相切的切线和杆
相切的切线和杆![]() .
.
因为![]() 垂直于平面
垂直于平面![]() ,所以
,所以![]() 垂直于切线。
垂直于切线。
又![]() 垂直于切线,所以支持力必在平面
垂直于切线,所以支持力必在平面![]() 内。
内。
如图丁所示,取![]() 的中点
的中点![]() ,连
,连![]() ,则
,则![]() ,取
,取![]() 的中点
的中点![]() ,连
,连![]() 。
。
![]() ,
,![]() ,
,
![]() 垂直于平面
垂直于平面![]() ,
,
![]() 平面
平面垂直于
![]() .
.
过![]() 作
作![]() 垂直于
垂直于![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,则
,则![]() 为支持力
为支持力![]() 的方向。
的方向。
因为杆![]() 的重力在平面
的重力在平面![]() 内,由三力交汇原理知,
内,由三力交汇原理知,![]() 处的全反力在平面
处的全反力在平面![]() 内,即
内,即![]() 与
与![]() 的合力在
的合力在![]() 内。
内。
![]() ,
, ![]() .
.
又平面![]() 垂直于平面
垂直于平面![]() ,
,
![]() 在平面
在平面![]() 中时,满足
中时,满足![]() .
.
![]() .
.
又![]() ,
,![]() ,
,
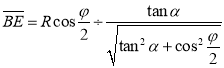 ,
,
又![]() ,
,
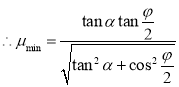 .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目