题目内容
【题目】碰撞后动能之和等于碰撞前动能之和的碰撞，称为弹性碰撞。
（1）质量分别为
，
的两个小球以同方向的速度
，
发生弹性碰撞，已知
，碰后速度分别记为
，
。假设碰撞是弹性碰撞，试列出方程求解得出，。
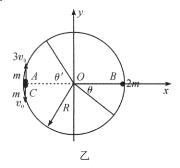
（2）光滑的水平桌面上平放着一个半径为R，内壁光滑的固定圆环，质量分别为m、2m、m的小球A、B、C在圆环内侧的位置和速度大小方向均在图甲中标出。初始B小球静止，已知所有碰撞为弹性碰撞。试问：经过多长时间，A、B、C三个小球又第一次恢复到原来位置？
【答案】（1）
， 
（2）
【解析】
（1）由动量守恒定律有
。
由碰撞前后动能之和保持不变有
。
联立解得，。
（2）建立以圆心为坐栝原点，AB方向为x轴正方向的平面直角坐标系，如图乙所示。小球A运动半周后与小球B发生碰撞。此过程经历时间为
。
设碰撞后小球A的速度为
，小球B的速度为
，规定逆时针方向为速度的正方向，由（1）问的结论可知
；
。
之后，小球B与小球C以时间
发生碰撞。由（1）问的结论可知碰撞后有
；
。
由
解得
。
在时间内，小球B转过的角度
。
小球B与小球C碰撞后，A、C两小球经时间
发生碰撞。由于两小球质量相等，碰撞后交换速度，有
；
。
由
解得
。
小球A转过的角度为
。
系统与初始状态的相对位置为顺时针转过了
。
所经历的时间为
。
要回到初始位置，设需要上述n个周期，则
，
解得
。
当
时，n有最小值，且
，故
。
练习册系列答案
相关题目
