Question

【题目】(2015·陕西）如图，AB切O于点D，直线AD交O于D，E两点，BC⊥DE，垂足为C．

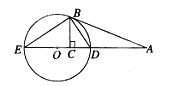
（1）证明：CBD=DBA；
（2）若AD=3DC，BC= ， 求O的直径．

Answer 1

【答案】
（1）

见解析。

（2）

3

【解析】∵DE是⊙O的直径，
则∠BED+∠EDB=90°，
∵BC⊥DE，
∴∠CBD+∠EDB=90°，即分∠CBA，
则BABC＝ADCD=3，
∵BC=2，
∴AB=32，AC=AB2-BC2＝4， 则AD=3， <即∠CBD=∠BED，
∵AB切⊙O于点B，
∴∠DBA=∠BED，即∠CBD=∠DBA；
（Ⅱ）由（Ⅰ）知BD平>由切割线定理得AB2=ADAE，
即AE=AB2AD＝6， 故DE=AE-AD=3，
即可⊙O的直径为3．
本题主要考查的是直径所对的圆周角、弦切角定理和切割线定理，属于容易题．解题时一定要注意灵活运用圆的性质，否则很容易出现错误．凡是题目中涉及长度的，通常会使用到相似三角形、全等三角形、正弦定理、余弦定理等基础知识