题目内容
【题目】有人提出了一种不用火箭发射人造地球卫星的设想．其设想如下：沿地球的一条弦挖一通道，如图甲所示．在通道的两个出口处A和B，分别将质量为M的物体和质量为m的待发射卫星同时自由释放，只要M比m足够大，碰撞后，质量为m的物体，即待发射的卫星就会从通道口B冲出通道．设待发卫星上有一种装置，在待发卫星刚离开出口B时，立即把待发卫星的速度方向变为沿该处地球切线的方向，但不改变速度的大小．这样待发卫星便有可能绕地心运动，成为一个人造卫星．若人造卫星正好沿地球表面绕地心做圆周运动，则地心到该通道的距离为多少？已知M=20m，地球半径
．假定地球是质量均匀分布的球体，通道是光滑的，两物体间的碰撞是弹性的．
【答案】
【解析】
位于通道内、质量为m的物体距地心O为r时（如图乙所示），它受到地球的引力可以R。表示为
①
式中
是以地心O为球心、以r为半径的球体所对应的那部分地球的质量，若以
表示地球的密度，此质量可以表示为
②
于是，质量为m的物体所受地球的引力可以改写为
． ③
作用于质量为m的物体的引力在通道方向的分力的大小为
， ④
， ⑤
为r与通道的中垂线OC间的卖角，x为物体位置到通道中点C的距离，力的方向指向通道的中点C．在地面上物体的重力可以表示为
⑥
式中
是地球的质量。由上式可以得到
． ⑦
由以上各式可以求得
． ⑧
可见，f与弹簧的弹力有同样的性质，相应的“劲度系数”为
． ⑨
物体将以C为平衡位置做简谐振动，振动周期为
．取x=0处为“弹性势能”的零点，设位于通道出口处的质量为m的静止物体到达x=0处的速度为
，则根据能量守恒，有
， ⑩
式中h表示地心到通道的距离．
解以上有关各式，得
可见，到达通道中点C的速度与物体的质量无关．
设想让质量为M的物体静止于出口A处，质量为m的物体静止于出口B处，现将它们同时释放，因为它们的振动周期相同，故它们将同时到达通道中点C处，并发生弹性碰撞．碰撞前，两物体速度的大小都是，方向相反，刚碰撞后，质量为M的物体的速度为V，质量为m的物体的速度为v，若规定速度方向由A向B为正，则有
，
解式和式，得
．
质量为m的物体是待发射的卫星，令它回到通道出口B处时的速度为u，则有
由式和⑨解得
u的方向沿着通道．根据题意，卫星上的装置可使u的方向改变成沿地球B处的切线方向，如果u的大小恰能使小卫星绕地球做圆周运动，则有
由式并注意到式⑥，可以得到，
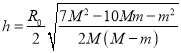
已知
，则得．
