Question

【题目】如图所示，长雪橇先在十分光滑的冰面上匀速滑行，然后滑上沥青马路，当滑行到雪橇长度一半时便停了下来，然后再从后面猛地一推，使雪橇具有与在冰面上滑行时相同的初速度，雪橇重新滑行一段后又停了下来.求雪橇两次减速的时间之比及减速的路程之比.

Answer 1

【答案】 ，

【解析】

雪橇在冰面上假设无摩擦，做匀速运动，其速度可以设为，进入沥青马路，作为初速度.

再设雪橇长为，质量为，当雪橇压在沥青马路上的长度为时，摩擦力为，其动力学方程为

.

这显然是简谐运动的回复力，其.

又由题意知：振幅.

所以，在这一过程中，减速时间与减速路程分别是

，.

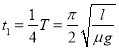下面讨论第二种情况：

由于这种情况下雪橇压在沥青马路上的长度变大，所以摩擦力变大，因此，在相同的初速度下，向右前进的距离会小于，这表示在停止之前，雪橇仍然只有部分进入沥青马路，故这一阶段的动力学方程与前一阶段相同.

假设在第二种情况下，雪橇也是从开始运动的，只是到达时雪橇的速度为，设在此情况下，在时雪橇的速度为，由能量关系有

.

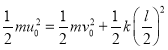所以，.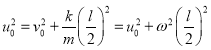

而，所以，，即.

第一种情况：

，.

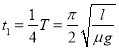第二种情况：

由能量关系有

，

则，.

设雪橇速度从变到耗时为，则

，.

所以，，，

即.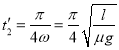

所以，.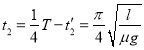

综上所述：

雪橇再次减速的时间之比为

；

减速的路程之比为

.

对于本题，必须特别说明的是解题过程中对能量关系式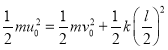的运用.

本题所给出的是一个含有摩擦力背景的模型，这是一个含有能量耗散的模型，在这一背景下，机械能是不存在守恒的，但上述式看上去却是典型的能量守恒式，我们该如何理解这一问题.

在简谐振动中，动能与其他形式的能量在相互转化，振动才能持续进行，如在弹簧振子中，动能与弹性势能的相互转化便导致了振动的持续进行，而且在这一过程中，动能与势能是保持守恒的.

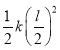而在这题所在背景下，是不存在与摩擦力相对应的势能的，表达式中的的部分也并非势能，它体现的是物体在摩擦力作用下消耗的动能大小，题中的关系式体现的是动能向其他形式的能量转化的关系，这种转化是通过摩擦力来实现的，换句话说，表达式反映的是在振动过程中动能向热能的转化关系.

如果仔细阅读解答中的表述，我们也不难发现，其表述用的是“能量关系”，而并非机械能守恒，所以，解答在能量的应用方面也不存在任何问题.

从本题的解答中，我们不难体会到，如果对振动过程中的能量特征没有深刻的认识，是无法做到突破“机械能守恒”的桎梏的.