题目内容
【题目】质量为![]() 、电量为
、电量为![]() 的电子从坐标原点
的电子从坐标原点![]() 不断地以大小都为
不断地以大小都为![]() 的速率沿不同方向射入
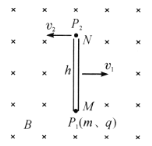
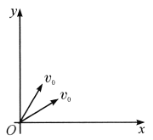
的速率沿不同方向射入![]() 平面的第一象限(见图).现要求加上一个垂直于
平面的第一象限(见图).现要求加上一个垂直于![]() 平面的匀强磁场,大小为
平面的匀强磁场,大小为![]() ,使所有这些电子穿出磁场后都能平行于
,使所有这些电子穿出磁场后都能平行于![]() 轴向
轴向![]() 方向运动,求符合条件的磁场最小面积.
方向运动,求符合条件的磁场最小面积.
【答案】![]()
【解析】
如图所示,在图上作任意两条电子运动的轨迹,圆弧末端切线与![]() 轴正向相同.设该末端坐标为
轴正向相同.设该末端坐标为![]() ,我们会发现
,我们会发现![]() 与
与![]() 关系满足以下的方程式:
关系满足以下的方程式:
![]() . ①
. ①
式中的![]() 是电子圆弧轨迹半径,
是电子圆弧轨迹半径,![]() .①式是个圆方程,圆心位置是
.①式是个圆方程,圆心位置是![]() ,圆半径是
,圆半径是![]() .遵从①式的所有点,构建了磁场的右边界.
.遵从①式的所有点,构建了磁场的右边界.
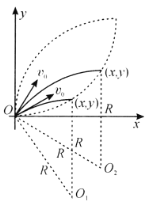
根据电子轨迹的一条极限位置,构建磁场的左边界.该电子从![]() 点向
点向![]() 方向射入,就一直沿这条边界运动,经
方向射入,就一直沿这条边界运动,经![]() 圆周后速度方向变为与
圆周后速度方向变为与![]() 轴正向相同.磁场的左右边界,共同构成了封闭的叶形,以第一象限的
轴正向相同.磁场的左右边界,共同构成了封闭的叶形,以第一象限的![]() 角平分线为对称轴,其面积
角平分线为对称轴,其面积![]() 的求法是
的求法是![]() (
(![]() 圆面积-腰长为
圆面积-腰长为![]() 的等腰直角三角形面积)
的等腰直角三角形面积)![]() .
.
本题虽然是一道高考试题,但它的思维特征却非常独到,在竞赛中更为常见.跟绝大多数训练题先给出匀强磁场,再研究带电粒子进入磁场后的轨迹和运动规律相反,本题的特点是先指定带电粒子的轨迹特征,再要求我们设计外加磁场的边界.这种训练是逆向的,思维是求异的,题型很新颖.
学科竞赛是极具选拔功能的,思维能力的高低最能甄别不同层面的学生,而且,对思维能力要求较高的试题也是优秀中学生最乐意研究与解答的试题,也是最受学生欢迎的试题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目