Question

【题目】已知函数f（x）=|x﹣2|．
（1）求不等式f（x）≤5﹣|x﹣1|的解集；
（2）若函数g（x）= ﹣f（2x）﹣a的图象在（ ，+∞）上与x轴有3个不同的交点，求a的取值范围．

Answer 1

【答案】
（1）解：不等式f（x）≤5﹣|x﹣1|，即|x﹣2|≤5﹣|x﹣1|，即|x﹣2|+|x﹣1|≤5，

∴ ①；或 ②；或 ．

解①求得﹣1≤x＜1，解②求得1≤x≤2，解求得 2＜x≤4，

综上可得，原不等式的解集为{x|﹣1≤x≤4}．

（2）若函数g（x）= ﹣f（2x）﹣a的图象在（ ，+∞）上与x轴有3个不同的交点，

则方程 ﹣f（2x）=a在（ ，+∞）上有3个解，

即函数h（x）= ﹣|2x﹣2|= 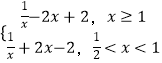的图象和直线y=a 在（ ，+∞）上有3个交点．

当 ＜x＜1时，f（x）= +2x﹣2≥2 ﹣2，当且仅当 =2x，即x= 时，等号成立．

再根据f（ ）=1=f（1），当x≥1时，f（x）= ﹣2x+2单调递减，如图所示：

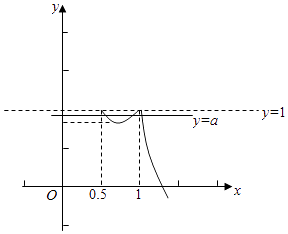
故a的取值范围为（2 ﹣2，1）．

【解析】（1）零点分区间讨论可得不等式解集，再取并集；（2）函数g（x）= ﹣f（2x）﹣a的图象在（ ，+∞）上与x轴有3个不同的交点,进行参变分离，即为，在上有3个解，根据数形结合得到a的取值范围.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点，需要掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号才能正确解答此题．