题目内容
【题目】设函数f(x)=|2x﹣2|+|x+3|.
(1)解不等式f(x)>6;
(2)若关于x的不等式f(x)≤|2a﹣1|的解集不是空集,试求a的取值范围.
【答案】
(1)解:f(x)= 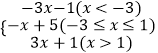
①由 ![]() ,解得x<﹣3;
,解得x<﹣3;
② ![]() ,解得﹣3≤x<﹣1;
,解得﹣3≤x<﹣1;
③ ![]() ,解得x>
,解得x> ![]() ;
;
综上可知不等式的解集为{x|x> ![]() 或x<﹣1}.
或x<﹣1}.
(2)解:因为f(x)=|2x﹣2|+|x+3|≥4,
所以若f(x)≤|2a﹣1|的解集不是空集,则|2a﹣1|≥f(x)min=4,
解得:a≥ ![]() 或a≤﹣
或a≤﹣ ![]() ..
..
即a的取值范围是:a≥ ![]() 或a≤﹣
或a≤﹣ ![]() .
.
【解析】1、去绝对值得到分段函数,根据题意f(x)>6,分别解出x的取值范围,最后取①②③得交集可得结果。
2、由f(x)=|2x﹣2|+|x+3|≥4自身的范围可知,若f(x)≤|2a﹣1|的解集不是空集,则|2a﹣1|≥f(x)min=4,,解得a的取值范围。
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目





