题目内容
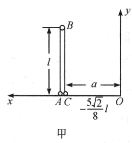
【题目】三个钢球A、B、C由两根轻质的长为l的硬杆连结，竖立在水平面上，如图甲所示，已知三球质量
，
，距杆
处有一面竖直墙。因受微小拢动，两杆分别向两边滑动，使B球下降，致使C球与墙面发生碰撞。设C球与墙面碰撞前后的速度大小不变，且所有摩擦不计，各球直径都比l小很多，求B落地瞬间三球的速度大小。
【答案】A、B、C三球的速度分别为：
、
和
。
【解析】
（1）．求球碰墙前三球的位置。
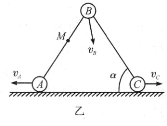
视A、B、C三者为一系统，A、C在水平面上滑动时，只要C不与墙面相碰，则此系统不受水平外力作用，此系统质心的水平坐标不发生变化。图乙所示为C球刚好要碰墙前三球的位置，以
表示此时BC杆与水平面间的夹角，则AB杆与水平面间的夹角也为，并令BA杆上的M点与系统质心的水平坐标相同，则应有
，
故得
。 ①
由上述知M点的水平坐标应与原来三球所在的位置的水平坐标相同，故知此刻M点与右侧墙面的距离即为a，即M点与C球的水平距离为a，由此有
，
即
，
由上式解得
，故有
。 ②
（2）求三球碰墙前的速度。
由于碰墙前M点的水平坐标不变，则在A、C沿水平面滑动过程中的任何时刻，由于图中的几何约束，C点与M点的水平距离总等于A点与M点的水平距离的
倍，可见任何时刻C点的水平速度大小总为A点水平速度大小的倍。以
、
、
分别表示图中三球的速度，则有
。 ③
又设沿BC方向的分量为
，则由于和分别为杆BC两端的小球速度，则此两小球速度沿着杆方向的投影应该相等，即span>V
。
再设沿BA方向的分量为
，同上道理可得
。
注意到BA与BC两个方向刚好互相垂直，故得的大小为
。
以②③两式代入上式，可得
。 ④
由于系统的机械能守恒，有
，
解方程可得
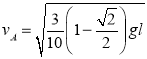。 ⑤
（3）求C球在刚碰墙后三球的速度。
如图丙所示，由于C球与墙碰撞，导致C球的速度反向而大小不变，由于杆BC对碰撞作用力的传递，使B球的速度也随之变化，这一变化的结果是：B球速度沿CB方向的分量
与C球速度沿CB方向的分量相等，即
。 ⑥
由于BC杆只能传递沿其杆身方向的力，故B球在垂直于杆身方向（即BA方向）的速度不因碰撞而发生变化，A球的速度也不因碰撞而发生变化，即其仍为。故得此时B球速度沿BA方向的分量
满足
。 ⑦
可得刚碰撞后B球速度大小为
。 ⑧
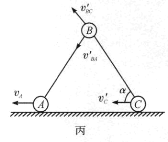
（4）求B球落地时三球的速度大小。
碰撞后，三球速度都有水平向左的分量。可见此后系统质心速度在水平方向的分量
应该方向向左，且由于此后系统不受水平外力，则应维持不变。由上解得的三球速度，可得应该满足
。
以③⑤⑥⑦诸式代入上式可解得
。 ⑨
当B球落地时，A、B、C三小球均在同一水平线上，它们沿水平方向的速度相等，显然，这速度也就是系统质心速度的水平分量。而B小球刚要落地时，A、C两球的速度均沿水平方向（即只有水平分量），B球的速度则还有竖直分量，以
表示此刻B球速度的大小。由系统的机械能守恒，有
。
由此可解得
。 ⑩
综合上述得本题答案为：当B小球刚落地时，A、B、C三球的速度大小分别为：、和。
