题目内容
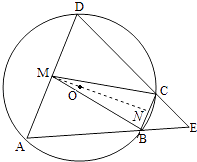
【题目】如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE. 
(1)证明:∠D=∠E;
(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.
【答案】
(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠D=∠CBE,
∵CB=CE,
∴∠E=∠CBE,
∴∠D=∠E;
(2)解:设BC的中点为N,连接MN,则由MB=MC知MN⊥BC,
∴O在直线MN上,
∵AD不是⊙O的直径,AD的中点为M,
∴OM⊥AD,
∴AD∥BC,
∴∠A=∠CBE,
∵∠CBE=∠E,
∴∠A=∠E,
由(1)知,∠D=∠E,
∴△ADE为等边三角形.
【解析】(1)利用四边形ABCD是⊙O的内接四边形,可得∠D=∠CBE,由CB=CE,可得∠E=∠CBE,即可证明:∠D=∠E;(2)设BC的中点为N,连接MN,证明AD∥BC,可得∠A=∠CBE,进而可得∠A=∠E,即可证明△ADE为等边三角形.

练习册系列答案
相关题目