题目内容
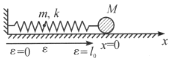
【题目】如图所示，劲度系数为
，质量为
的均匀水平弹簧一端固定，另一端连接质量为
的小球，小球与水平地面间无摩擦.让小球偏离平衡位置
点，自由释放后便可沿图示的
轴振动，在弹簧无形变时，以弹簧的固定端为原点，沿弹簧设置向右的
坐标.设小球振动量为时，弹簧中原点的振动量（即相对其初始位置的位移量）为
，式中
是弹簧的自由长度.这一假设也可简单地说成：弹簧各处振动量与小球振动量成正比，作此假设后，试求小球的振动周期
.
【答案】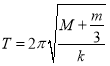
【解析】
弹簧为原长
时，在
邻域取
段，它的质量为
.
小球从平衡位置
点移到
时，弹簧段相对其初始位置的位移量为
，若小球振动速度为
，则弹簧段的振动速度为
.
具有的动能为
.
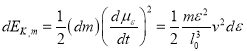整个弹簧的动能便是
.
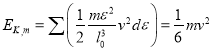系统总能量为
，
.
对上式两边求导可得：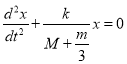
.
则小球振动的角频率和周期分别为
，.
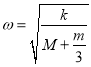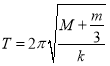对于理想模型弹簧振子，我们通常只需交代一句“轻弹簧”足矣，即无须考虑能与振动的弹簧的质量，这显然是一种近似，是一种理想化.然而，在具体的情境中，弹簧的质量往往是不能忽视的，而且，它也是参与振动，更加复杂的是，弹簧上各点的振动周期虽然相同，但振动的幅度却并不相同，如果用动力学思想来求解振动的系数
，难度是较大的，而能量分析法在此又显现出巨大的作用.
本题的结果也是值得大家注意的，若考虑弹簧的质量，则只需在振子质量上加上弹簧质量的
即可，系统仍等效为一个理想的弹簧振子.此外，这一结论在实验操作中也是必须考虑的.
练习册系列答案
相关题目
