题目内容
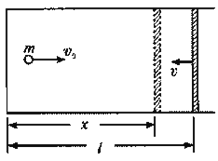
【题目】在两个相接触的肥皂泡融合前,常有一个中间阶段,即在两个肥皂泡之间产生一层薄膜,如图甲所示。

(1)曲率半径![]() 和
和![]() 已知,求把肥皂泡分开的薄膜的曲率半径;
已知,求把肥皂泡分开的薄膜的曲率半径;
(2)考虑![]() 的特殊情况,在中间状态形成前,肥皂泡的半径多大?在中间膜消失后,肥皂泡的半径多大?我们假定,肥皂泡里的超压只与表面张力及半径有关,而且比大气压小得多,因此泡内的气体体积不会改变。
的特殊情况,在中间状态形成前,肥皂泡的半径多大?在中间膜消失后,肥皂泡的半径多大?我们假定,肥皂泡里的超压只与表面张力及半径有关,而且比大气压小得多,因此泡内的气体体积不会改变。
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)设肥皂液的表面张力系数为σ,则液泡内的超压为![]() 。因此半径小的液泡内的超压较大,泡内气体的压强也比较大。所以连体过渡泡的中间隔膜应向半径较大的泡一边凸出。
。因此半径小的液泡内的超压较大,泡内气体的压强也比较大。所以连体过渡泡的中间隔膜应向半径较大的泡一边凸出。
设中间隔膜的曲率半径为![]() ,则该曲面产生的附加压强为
,则该曲面产生的附加压强为![]() ,为了使中间状态的隔膜保持平衡,应有
,为了使中间状态的隔膜保持平衡,应有![]() ,即
,即![]() 。
。
(2)当![]() 时,隔膜的曲率半径
时,隔膜的曲率半径![]() ,即是一个平面,在界线上任取一点A,它受到两个球面及薄膜的表面张力
,即是一个平面,在界线上任取一点A,它受到两个球面及薄膜的表面张力![]() 、
、![]() 、
、![]() 均跟各面相切,如图乙所示。由于是同一种液体,故三力大小
均跟各面相切,如图乙所示。由于是同一种液体,故三力大小![]() ,平衡时它们的方向彼此夹120°角,
,平衡时它们的方向彼此夹120°角,![]() 应组成等边三角形,“球幅”的高度
应组成等边三角形,“球幅”的高度![]() ,所以每个过渡泡的体积为
,所以每个过渡泡的体积为
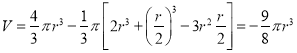 。
。
而压强![]() 。
。
设生成过渡泡前的肥皂泡半径为R,则
![]() ,
,![]() 。
。
生成大泡的半径为![]() ,则
,则
![]() ,
,![]() 。
。
依据玻意耳定律有
![]() ,
,
![]() 。
。
若考虑到![]() ,则泡内气体总体积可认为不变,故可近似得出
,则泡内气体总体积可认为不变,故可近似得出![]() ,
,![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目