题目内容
【题目】有一根玻璃棒，材料折射率为
，横截面为等边三角形.在一张白纸上画一组平行直线，如图所示，将棒置于平行线上，棒轴与平行线夹角为
.如果人在玻璃棒上方较远处垂直纸面观察，试讨论：当取哪些不同的值时，人通过玻璃棒将会看到什么样的图像？画出这些情况下人看到的图像的形状.
注：除全反射外不考虑其他反射，分析过程不做要求，给出的取值范围和对应的图像形状即可.
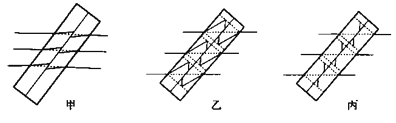
【答案】（1）
时，图像如图甲所示（2）
时，图像如图乙所示（3）
时，图像如图丙所示。
【解析】
因为人在离玻璃棒较远处垂直纸面观察，所以射出玻璃棒的光只有垂直于纸面才能被人观察到.考察这些光线在玻璃棒中的折射和全反射情况，由于对称性只考虑从一侧（右侧）射出的光
当折射率
较小时，光路如图1所示，所有从右侧射出的光都是由底边直接射过来的，由图可知，实际看到点的位置比实际位置更加靠右（棱镜底边），比如从
、
、
点射出的光经棱镜折射后，实际成像是在
、
、
点.据此分析，可画出此情况下人观察到的图像，如图2，图中虚线为被玻璃棒挡住的部分，不一定要画出，
当玻璃的折射率比较大时，垂直纸面射出的光不再全是由底面直接折射而出，而会有一部分光线是先通过左侧全反射后再由右侧折射而出，如图4所示.而作为临界情况，光路如图3所示，容易求得图3光路达成的条件是
.所以可以确定图1光路和图2图像形成的条件为。
现在分析
时的情况（时容易验证左侧一定会发生全反射）.由底面射出直接折射而出的光线，其视觉效果应与图2一样；而通过左侧全反射再由右侧折射出的光，其形成的图线走向应与图2相反.所以可画出图；像如图5所示，虚线为辅助线，不必一定画出.；当折射率进一步增大时，如图4所示，
角不断减小，而
角不断增加，角为从纸面经空气进入玻璃的折射角，根据折射规律，角最多为
，所以当足够大时，不会再有光线能够从底面进入玻璃棒直接从右侧射出且被人看到.现在求此情况出现的临界条件.
由
，
，
可得
.
所以图5所示的图像应为时的情况.当时，图4中直接折射而出的那些光路不再存在，图像应为图6所示，
几何光学无疑要求答题都具备较强的几何驾驭能力，包含着空间问题的驾驭能力.可以说，本题是鉴别学生空间问题处理能力与几何能力强弱的典型试题.它除了要求答题者能对“人在玻璃棒上方较远处垂直纸面观察”的描述还原成出射光线垂直于纸面外，答题者还必须对形成这样的出射光线的光路的走向，实际看到影像的平面特征作出正确的分析判断，答题者如无极强的空间想象力与严谨的思维能力，则无法对其光路作出正确的描述与呈现.同时，棱镜不同的折射率又直接影响着全反射的发生与出射的光路，从而影响到图像呈现的平面形态，而这又要求答题者具备极为严谨而又全面的思维及处理光的折射计算的能力，所以，本题是一道综合能力很强，难度极大的试题.本题还存在着一种变式，即将本题中的三棱玻璃棒换成圆柱形玻璃棒，再来讨论相关问题，读者不妨作相应的延伸与讨论。
