题目内容
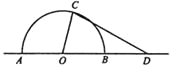
【题目】如图,某城市有一块半径为40![]() 的半圆形(以
的半圆形(以![]() 为圆心,
为圆心, ![]() 为直径)绿化区域,现计划对其进行改建,在
为直径)绿化区域,现计划对其进行改建,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,在半圆上选定一点
,在半圆上选定一点![]() ,改建后的绿化区域由扇形区域
,改建后的绿化区域由扇形区域![]() 和三角形区域
和三角形区域![]() 组成,其面积为
组成,其面积为![]() ,设
,设![]()
(1)写出![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)试问![]() 多大时,改建后的绿化区域面积
多大时,改建后的绿化区域面积![]() 最大.
最大.
【答案】(1)S=1600sinx+800x,0<x<π;(2)当∠AOC为![]() 时,改建后的绿化区域面积S最大.
时,改建后的绿化区域面积S最大.
【解析】试题分析:(1)求出扇形区域AOC、三角形区域COD的面积,即可求出S关于x的函数关系式S(x),并指出x的取值范围;(2)求导数,确定函数的单调性,即可得出结论
试题解析:(1)因为扇形 AOC的半径为 40 m,∠AOC=x rad,
所以 扇形AOC的面积S扇形AOC=![]() =800x,0<x<π. ………………… 2分
=800x,0<x<π. ………………… 2分
在△COD中,OD=80,OC=40,∠COD=π-x,
所以△COD 的面积S△COD=![]() ·OC·OD·sin∠COD=1600sin(π-x)=1600sinx.……………… 4分
·OC·OD·sin∠COD=1600sin(π-x)=1600sinx.……………… 4分
从而 S=S△COD+S扇形AOC=1600sinx+800x,0<x<π. ………… 6分
(2)由(1)知,S(x)=1600sinx+800x,0<x<π.
S′(x)=1600cosx+800=1600(cosx+![]() ). ………… 8分
). ………… 8分
由 S′(x)=0,解得x=![]() .
.
从而当0<x<![]() 时,S′(x)>0;当
时,S′(x)>0;当![]() <x<π时, S′(x)<0 .
<x<π时, S′(x)<0 .
因此 S(x)在区间(0, ![]() )上单调递增;在区间(
)上单调递增;在区间(![]() ,π)上单调递减. ……………… 11分
,π)上单调递减. ……………… 11分
所以 当x=![]() ,S(x)取得最大值.
,S(x)取得最大值.
答:当∠AOC为![]() 时,改建后的绿化区域面积S最大. ……………… 14分
时,改建后的绿化区域面积S最大. ……………… 14分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目