Question

【题目】如图甲所示，空间有一半径为R的介质球体，球体左半部分均匀带有静止电荷，总电量为，右半部分也均匀带有静止电荷，总电量为，试求全空间的平均场强．首先说明平均电场的含义：将体积为V的空间区域分解为一系列的小区域，第i个小区域的体积为无限小量，该区域的电场强度为，则V区域的平均电场强度为

Answer 1

【答案】全空间平均场强为零

【解析】

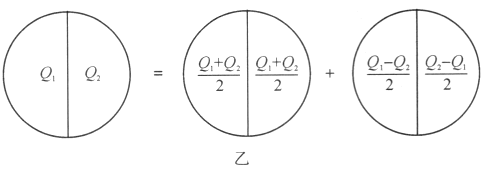
方法1：将原带电球分解为两个带电体体系之和，如图乙所示。第一个体系为带电量是的球对称体系，它在全空间的平均场强显然为零。第二个体系是带等量异号电荷的反对称体系，它在全空间平均场强也为零。因此，原带电球在全空间平均场强为零．

方法2：球体的这种带电方式并不对称，但是若在其中取一个半径为无穷小的带电小球，这一小球在全空间的场强便具有球对称性，对应的平均场强必为零，即有．

原带电球体分解为一系列无穷小带电小球后，便将表面上看来并不对称的原问题转化为包含对称性的问题．原带电球体全空间场强E为一系列的叠加，即有．

于是．