题目内容
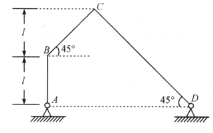
【题目】如图为用三角形刚性细杆AB、BC、CD连成的平面连杆结构图。AB杆和CD杆可分别绕过A、D的垂直于纸面的固定轴转动，A、D两点位于同一水平线上。BC杆的两端分别与AB杆和CD杆相连，可绕连接处转动（类似铰链）。当AB杆绕A轴以恒定的角速度
转到图中所示的位置时，AB杆处于竖直位置。BC杆与CD杆都与水平方向成
角，已知AB杆的长度为l，BC杆和CD杆的长度由图给定。求此时C点加速度
的大小和方向（用与CD杆之间的夹角表示）。
【答案】
，
的方向与杆CD间的夹角为
【解析】
因为B点绕A轴做圆周运动,其速度的大小为
. ①
B点的向心加速度的大小为
. ②
因为是匀角速转动,B点的切向加速度为0,故
也是B点的加速度,其方向沿BA方向.因为C点绕D轴做圆周运动,其速度的大小用
表示,方向垂直于杆CD,在考察的时刻,由图乙可知,方向沿杆BC方向.因BC是刚性杆,所以B点和C点沿BC方向的速度必相等,故有
。 ③
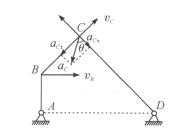
此时杆CD绕D轴按顺时针方向转动,C点的法向加速度为
。 ④
由图甲可知
,由③④式得
， ⑤
其方向沿CD方向。
下面来分析C点垂直于杆
方向的加速度,即切向加速度
.因为
是刚性杆,所以C点相对B点的运动只能是绕B点的转动,C点相对B点的速度方向必垂直于杆.令
表示其速度的大小,根据速度合成公式有
。
由几何关系得
。
由于C点绕B点做圆周运动，相对B点的向心加速度为
。
因为
，
故有
，其方向垂直于杆。
由②式及图可知,B点的加速度沿杆的分量为
,
所以,C点相对A点(或D点)的加速度垂直于杆方向的分量为
。
C点的总加速度为C点绕D点做圆周运动的法向加速度
与切向加速度的合加速度,即
。
的方向与杆间的夹角为
。
本题是第24届全国中学生物理竞赛复赛试题。
本题的模型亦是平面铰接的构件,在一般的训练中,涉及变形问题的只有两杆件,杆件上各处的速度与加速度的关系比较直接,而本题给出了三个可变形杆件,且上没有固定点或恒定的速度点,其运动的关联便显得更为复杂,其相对运动的关系(主要是相对加速度)更难把握我们可以本题的分析为例,掌握分析与解答此类问题的方法。
