Question

【题目】内半径为R的直立圆柱器皿内盛水银，绕圆柱轴线匀速旋转（水银不溢，皿底不露），稳定后的液面为旋转抛物面。若取坐标原点在抛物面的最低点，纵坐标轴r与圆柱器皿的轴线重合，横坐标轴r与z轴垂直，则液面的方程为，式中为旋转角速度，g为重力加速度（当代已使用大面积的此类旋转水银液面作反射式天文望远镜）。观察者的眼睛位于抛物面最低点正上方某处，保持位置不变，然后使容器停转，待液面静止后，发现与稳定旋转时相比，看到的眼睛的像的大小、正倒都无变化。求人眼位置至稳定旋转水银面最低点的距离。

Answer 1

【答案】

【解析】

旋转抛物面对平行于对称轴的光线严格聚焦，此抛物凹面镜的焦距为。

由上式，旋转抛物面方程可表示为。

停转后液面水平静止，由液体不可压缩性，知液面上升。以下求抛物液面最低点上升的高度。

抛物液面最低点以上的水银，在半径R、高的圆柱形中占据体积为Μ的部分，即附图中左图阴影部分绕轴线旋转所得的回转体，其余体积为V的部分无水银。体Μ在高度z处的水平截面为圆环，利用抛物面方程，得z处圆环面积为

。

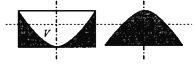
将体V倒置，得附图中右图阴影部分绕轴线旋转所得的回转体Λ，相应抛物面方程变为，其高度z处的水平截面为圆面，面积为

。

由此可知：，

即停转后抛物液面最低点上升: 。

因抛物镜在其轴线附近的一块小面积可视为凹球面镜，抛物镜的焦点就是球面镜的焦点，故可用球面镜的公式来处理问题。两次观察所见到的眼睛的像分别经凹面镜与平面镜反射而成，而先后看到的像的大小、正倒无变化，这就要求两像对眼睛所张的视角相同。设眼长为，凹面镜成像时，物距u即所求距离，像距v与像长y分别为

平面镜成像时，由于抛物液面最低点上升，物距为。

像距与像长分别为。

两像视角相同要求。

利用上述诸式，可解得所求距离。