题目内容
【题目】已知圆C1：x2+y2+6x=0关于直线l1：y=2x+1对称的圆为C
（1）求圆C的方程；
（2）过点（﹣1，0）作直线与圆C交于A，B两点，O是坐标原点，是否存在这样的直线，使得在平行四边形OASB中| 
|=| 
﹣ 
|？若存在，求出所有满足条件的直线的方程；若不存在，请说明理由．
【答案】
（1）解：圆C1：x2+y2+6x=0化为标准方程为（x+3）2+y2=9，
设圆C1的圆心C1（﹣3，0）关于直线l1：y=2x+1的对称点为C（a，b），
则 
，且CC1的中点M（ 
， 
）在直线l1：y=2x+1上．
∴ 
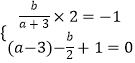，解得 
．
∴圆C的方程为（x﹣1）2+（y+2）2=9；
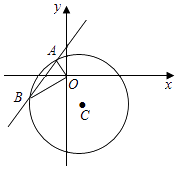
（2）如图：设A（x1，y1），B（x2，y2）．
由| 
|=| 
﹣ 
|= 
，得四边形OASB为矩形，∴OA⊥OB，
必须使 
，即x1x2+y1y2=0．
①当直线的斜率不存在时，可得直线的方程为x=﹣1，
与圆C：（x﹣1）2+（y+2）2=9交于两点A（﹣1， 
），B（﹣1， 
）．
∵ 
，
∴OA⊥OB，
∴当直线的斜率不存在时，直线l：x=﹣1满足条件；
②当直线的斜率存在时，可设直线的方程为y=k（x+1），
设A（x1，y1），B（x2，y2），
由 
，得（1+k2）x2+（2k2+4k﹣2）x+k2+4k﹣4=0，
由于点（﹣1，0），在圆C内部，∴△＞0恒成立，
∴ 
， 
，
由x1x2+y1y2=0，得 
，
整理得 
，
解得k=1，∴直线方程为y=x+1，
∴存在直线x=﹣1和y=x+1，它们与圆C交A，B两点，且| |=| ﹣ |．
【解析】（1）将圆C的一般方程写成标准方程，找出圆心坐标及半径，再根据对称，找到对称的圆心坐标，从而得出对称圆的方程；（2）设A（x1，y1），B（x2，y2），根据向量关系不难得出OASB为矩形，可得出OA⊥OB，分斜率存在与斜率不存在，设出直线方程，联立圆的方程，根据韦达定理，得出满足题意的直线方程.
【考点精析】认真审题，首先需要了解直线与圆的三种位置关系(直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点)．
