题目内容
【题目】设f(x)=|x﹣1|+|x+1|,(x∈R)
(1)求证:f(x)≥2;
(2)若不等式f(x)≥ ![]() 对任意非零实数b恒成立,求x的取值范围.
对任意非零实数b恒成立,求x的取值范围.
【答案】
(1)证明:f(x)=|x﹣1|+|x+1|=|1﹣x|+|x+1|≥|1﹣x+x+1|=2
(2)解:g(b)= 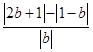 ≤
≤ ![]() =3,
=3,
∴f(x)≥3,即|x﹣1|+|x+1|≥3,
x≤﹣1时,﹣2x≥3,∴x≤﹣1.5,∴x≤﹣1.5;
﹣1<x≤1时,2≥3不成立;
x>1时,2x≥3,∴x≥1.5,∴x≥1.5.
综上所述x≤﹣1.5或x≥1.5
【解析】(1)利用三角不等式证明:f(x)≥2;(2)g(b)= ![]() ≤
≤ ![]() =3,可得f(x)≥3,即|x﹣1|+|x+1|≥3,分类讨论,求x的取值范围.
=3,可得f(x)≥3,即|x﹣1|+|x+1|≥3,分类讨论,求x的取值范围.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目