题目内容
【题目】设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a,b∈M.
(Ⅰ)证明:| ![]() a+
a+ ![]() b|<
b|< ![]() ;
;
(Ⅱ)比较|1﹣4ab|与2|a﹣b|的大小.
【答案】解:(Ⅰ)记f(x)=|x﹣1|﹣|x+2|= 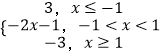 ,
,
由﹣2<﹣2x﹣1<0解得﹣ ![]() <x<
<x< ![]() ,则M=(﹣
,则M=(﹣ ![]() ,
, ![]() ).
).
∵a、b∈M,∴|a|< ![]() ,|b|<
,|b|< ![]() ,
,
∴| ![]() a+
a+ ![]() b|≤
b|≤ ![]() |a|+
|a|+ ![]() |b|<
|b|< ![]() .
.
(Ⅱ)由(Ⅰ)得a2< ![]() ,b2<
,b2< ![]() .
.
因为|1﹣4ab|2﹣4|a﹣b|2=(1﹣8ab+16a2b2)﹣4(a2﹣2ab+b2)
=(4a2﹣1)(4b2﹣1)>0,
所以|1﹣4ab|2>4|a﹣b|2,故|1﹣4ab|>2|a﹣b|.
【解析】(I)先解绝对值不等式,再利用绝对值三角不等式可证明| ![]() a+
a+ ![]() b|<
b|< ![]() ;(II)由(I)可得a2和b2,利用作差法比较|1﹣4ab|2与4|a﹣b|2的大小,从而可得|1﹣4ab|与2|a﹣b|的大小.
;(II)由(I)可得a2和b2,利用作差法比较|1﹣4ab|2与4|a﹣b|2的大小,从而可得|1﹣4ab|与2|a﹣b|的大小.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).

练习册系列答案
相关题目