题目内容
【题目】已知函数f(x)为二次函数,满足f(0)=1,且f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)若方程f(2x)=2x+a在x∈(﹣∞,2]上有两个不同的解,求实数a的取值范围.
【答案】
(1)解:设f(x)=ax2+bx+c,由f(0)=1得c=1,
∴f(x)=ax2+bx+1,
∴f(x+1)=a(x+1)2+b(x+1)+1=ax2+(2a+b)x+a+b+1,
∴f(x+1)﹣f(x)=ax2+(2a+b)x+a+b+1﹣ax2﹣bx﹣1
=2ax+a+b,
∵f(x+1)﹣f(x)=2x,
∴2ax+a+b=2x,
∴2a=2且a+b=0,
∴a=1,b=﹣1,
∴f(x)=x2﹣x+1
(2)解:若方程f(2x)=2x+a在x∈(﹣∞,2]上有两个不同的解,
即a=(2x﹣1)2在x∈(﹣∞,2]上有两个不同的解,
令t=2x,则0<t≤4,
令g(t)=(t﹣1)2,
画出函数g(t)和y=a的图象,如图所示:
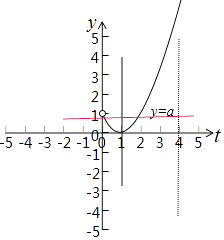
故0<a<1.
【解析】(1)设出函数f(x)的解析式,根据f(0)=1求出c的值,根据f(x+1)﹣f(x)=2x,求出a,b的值,从而求出函数的解析式即可;(2)问题转化为a=(2x﹣1)2在x∈(﹣∞,2]上有两个不同的解,令t=2x,则0<t≤4,令g(t)=(t﹣1)2,画出函数g(t)和y=a的图象,读出a的范围即可.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目