题目内容
【题目】已知函数 ![]() 在区间
在区间 ![]() 上有最大值4和最小值1.设
上有最大值4和最小值1.设 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上恒成立,求实数
上恒成立,求实数 ![]() 的取值范围.
的取值范围.
(3)若 ![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:因为 ![]() 的对称轴为
的对称轴为 ![]() ,且
,且 ![]() ,故函数
,故函数 ![]() 在区间
在区间 ![]() 上单调递增,则由题设
上单调递增,则由题设 ![]() ,即
,即 ![]()
(2)解:由(1)可知 ![]() ,则
,则 ![]() 可化为
可化为 ![]() ,即
,即 ![]() ,令
,令 ![]() ,由于
,由于 ![]() ,所以
,所以 ![]() ,则不等式可化为
,则不等式可化为 ![]() 在
在 ![]() 上恒成立.记
上恒成立.记 ![]() ,因其对称轴为
,因其对称轴为 ![]() ,故
,故 ![]() ,所以
,所以 ![]() ,即所求实数
,即所求实数 ![]() 的取值范围是
的取值范围是 ![]()
(3)解:因 ![]() ,故
,故 ![]() ,则原方程可化为
,则原方程可化为 ![]() ,令
,令 ![]() , 由于
, 由于 ![]() ,则
,则 ![]()
所以问题转化为方程 ![]() 有两个不相等的实数根
有两个不相等的实数根 ![]() ,其中
,其中 ![]() 或
或 ![]() ,记
,记 ![]() ,结合该二次函数图象可得:
,结合该二次函数图象可得: ![]() 或
或 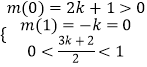 ,解之得
,解之得 ![]() 或
或 ![]() ,则
,则 ![]() ,故所求实数的取值范围是
,故所求实数的取值范围是 ![]()
【解析】(1)由二次函数的性质可知 g(x) 在指定区间上是增函数,结合题中的已知条件得到关于a、b的方程组求解即可(2)整理化简原不等式,令t=![]() 则原函数化为 h(t)一个关于t的二次函数,再由t自身的条件限制得出t的取值范围,从而得出k的取值范围即可。(3)整体思想令| 2x 1 | = u化简整理方程可得出关于u的方程,根据方程有两个不同的根u1 , u2,结合二次函数的性质得出两个特殊点的函数值的正负 ,进而得到关于k的不等式组,解出即可得到k的取值范围。
则原函数化为 h(t)一个关于t的二次函数,再由t自身的条件限制得出t的取值范围,从而得出k的取值范围即可。(3)整体思想令| 2x 1 | = u化简整理方程可得出关于u的方程,根据方程有两个不同的根u1 , u2,结合二次函数的性质得出两个特殊点的函数值的正负 ,进而得到关于k的不等式组,解出即可得到k的取值范围。
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目