题目内容
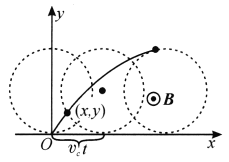
【题目】如图所示，空间有互相正交的匀强电场
和匀强磁场
，沿
方向，沿
方向．一个带正电
、质量为
的粒子（设重力可以忽略），从坐标原点
开始无初速出发，求粒子坐标和时间的函数关系，以及粒子的运动轨迹．
【答案】①
②
③粒子的运动轨迹为旋轮线
【解析】
粒子从
点起无初速出发，受恒定电场力作用沿
方向运动．因为速度
的大小、方向都改变的洛仑兹力仅在
平面上起作用，粒子轨迹一定不会离开平面且一定以为起点，既然粒子仅受的两个力中，一个是恒力，一个是变力，利用独立性与叠加原理，我们设想把洛仑兹力分解为两个分力，使一个分力跟恒电场力抵消，这就把实际受力简化为只受一个洛仑兹力分力的问题。注意此处不是场的分解和抵消，而是通过先分解速度再达到对力进行分解和叠加．
我们都知道，符合一定大小要求的彼此正交的匀强复合电磁场能起速度选择器作用．受其原理启发，设想粒子从点起（此处
）就有一个沿
轴正方向、大小为
的始终不变的速度．当然在点同时应有一个沿
方向的大小也是
的速度，保证在点，则
，
沿
方向，
沿方向，彼此抵消，可写成
．因任一时刻
，所以，
，或改写成：
．式中的三个速度和三个
都在平面上，其物理意义是：粒子在复合场中受的两个真实的力
和
的矢量和，可以用一个洛仑兹力分力
来代替，这样做的一个先决条件是把粒子运动看成以下两个分运动的合成：
①沿
方向的
的匀速直线运动；
②在平面上的一个匀速圆周运动．
其理由是：是平面力，轨迹又是平面的而不是三维空间的，所以必与
垂直，在点就是
，之后不对粒子做功，大小不变，充当向以力．这个圆周运动特征量是
，
，
．
时刻，粒子位于点，此时起粒子具有两个速度：一是之后方向始终不变、大小为的速度．由这个速度引起的洛仑兹力跟电场力抵消，另一个速度是在点时沿方向的大小为
的速度，该速度引起的洛仑兹力指向
点，这点就时的圆心．之后该圆心以速率
沿平行于轴正向的方向无滑动开始平动，粒子是该圆周上的一个点，且时恰好就是该圆与轴的切点即坐标原点，此后，粒子相对圆心以角速度
顺时针绕行，如图乙所示．在平面上，粒子的运动轨迹被称为旋轮线，其坐标值随时间变化的参数方程为
， ①
， ②
． ③
本题是物理竞赛试题中最经典的试题之一．
首先，本题解答中对粒子运动状态的处理，既特别又具有典型性．即在粒子的运动中分解出一个匀速直线运动，使其因运动而受到的洛仑兹力与其受到的恒定电场力（有的模型中为粒子的重力）构成平衡，从而粒子的运动是一个匀速直线运动与一个匀速圆周运动的合成．
其次，本题问题设置的可塑性很大．至少，粒子初速度的设置就可能导致轨迹方程表述的复杂程度发生大的变化，还有可能涉及过程中物理量的讨论与计算，如加速度、曲率半径等．
再次，本题中粒子的轨迹方程是旋轮线，物理中围绕旋轮线能做大量的文章，如对形成此类轨迹的力学模型的研究，它与等时摆线的关系．
最后，有一定数学能力的学生，不妨尝试把参数
消去得出
与的关系式，用来表示其轨迹的方法，并在此基础上研究等时摆．
总之，竞赛学习过程中，深挖此题的功能，一定会有较大的收获．
