题目内容
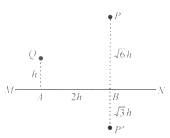
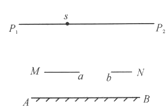
【题目】图中AB表示一个水平放置的平面镜,![]()
![]() 是水平放置的米尺(有刻度的一面朝着平面镜),MN是屏,三者互相平行,屏MN上的ab表示一条竖直的缝(即a、b之间是透光的)。某人眼睛紧贴米尺上的小孔s(其位置见图),可通过平面镜看到米尺的一部分刻度,试在本题的图上用三角板作图求出可看到的部位,并在
是水平放置的米尺(有刻度的一面朝着平面镜),MN是屏,三者互相平行,屏MN上的ab表示一条竖直的缝(即a、b之间是透光的)。某人眼睛紧贴米尺上的小孔s(其位置见图),可通过平面镜看到米尺的一部分刻度,试在本题的图上用三角板作图求出可看到的部位,并在![]()
![]() 上把这部分涂以标志。
上把这部分涂以标志。
【答案】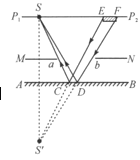
【解析】
本题考查平面镜成像规律及成像作图。人眼通过小孔看见的是米尺刻度的像。由反射定律可知,米尺刻度必须经过平面镜反射后,反射光线进入人的眼睛,人才会看到米尺刻度的像。可以通过两种方法来解这个问题。
方法一:相对于平面镜AB作出人眼S的像![]() 连接Sa并延长交平面镜于点C,连接
连接Sa并延长交平面镜于点C,连接![]() 与点C并延长交米尺
与点C并延长交米尺![]() 于点E:,点E就是人眼看到的米尺刻度的最左端;连接
于点E:,点E就是人眼看到的米尺刻度的最左端;连接![]() 并延长交米尺
并延长交米尺![]() 于点F,
于点F,![]() 与平面镜交于点D,连接S与点D,则点F就是人眼看到的米尺刻度的最右端。Ε与F之间的米尺刻度就是人眼可看到部分,如图乙所示。
与平面镜交于点D,连接S与点D,则点F就是人眼看到的米尺刻度的最右端。Ε与F之间的米尺刻度就是人眼可看到部分,如图乙所示。
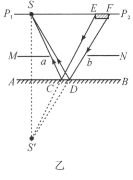
方法二:根据平面镜成像的对称性,作米尺![]() 及屏MN的像,分别是
及屏MN的像,分别是![]() 及
及![]() ,a、b的像分别为
,a、b的像分别为![]() ,
,![]() ,如图丙所示。连接Sa交AB于点C,延长并交
,如图丙所示。连接Sa交AB于点C,延长并交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() (AB)的垂线,交于点E,此点就是人眼看到的米尺刻度的最左端;连接
(AB)的垂线,交于点E,此点就是人眼看到的米尺刻度的最左端;连接![]() 交AB于点D,延长并交
交AB于点D,延长并交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() (AB)的垂线
(AB)的垂线![]() 交于点F,点F就是人眼看到的米尺刻度的最右端。EF部分就是人眼通过平面镜可看见的米尺部分。
交于点F,点F就是人眼看到的米尺刻度的最右端。EF部分就是人眼通过平面镜可看见的米尺部分。
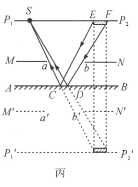

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目