题目内容
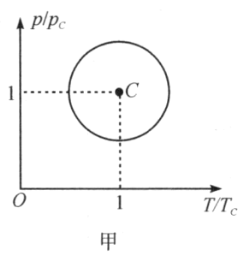
【题目】如图甲所示是一定量理想气体状态变化所经历的
图线，该图线是以C点为圆心的圆,p轴是以
为单位，Τ轴以
为单位。、分别是C点压强和热力学温度。若已知在此过程中气体所经历的最低温度为
，则在此过程中，气体密度的最大值
和最小值
的比值
应等于多少？
【答案】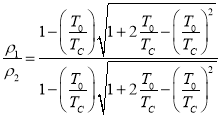
【解析】
由理想气体状态方程
得到
。
对于一定量的气体，C是一个常数。
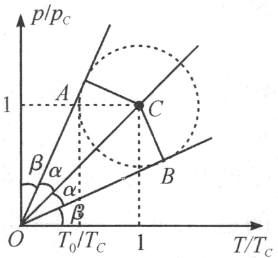
由上式可知，在
图上，一定量理想气体的等容过程是由一条过原点O的直线来表示的，而且该气体的体积愈大，表示等容过程的直线的斜率愈小，因此判断在题图给出的圆过程中何点气体密度最小、何点密度最大时，可由原点O对该圆作一系列相交的直线，如图乙所示，其中斜率最大的直线为与圆上方相切的切线OA,斜率最小的直线为与圆下方相切的切线OB，由此可知该一定量气体在变化过程中，在切点Α,该气体的体积最大，在切点Β，该气体的体积最小，对一定量气体来说，其密度与体积成反比，即
。
其中，
、
分别是该气体在Α、B点的体积，设以
和
、和
分别表示该气体在Α、B点的压强和温度，则由理想气体状态方程得到
。
代入上式得到
。
上式可改写成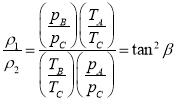
。
角β的意义如图乙所示，从图中可以看出
，故上式可改写成
。
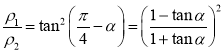由图中可以看出
，CB是圆的半径r，
，
。代入上式并化简，可得到
。
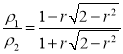由图可以看出，圆的半径r与在变化过程中的气体所经历的最低温度
的关系是
。
将此关系代入上式就可得到
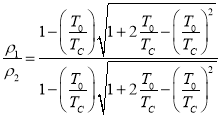
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
