题目内容
【题目】如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. 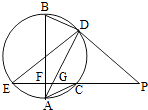
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED.
【答案】
(1)证明:∵PG=PD,∴∠PDG=∠PGD,
∵PD为切线,∴∠PDA=∠DBA,
∵∠PGD=∠EGA,
∴∠DBA=∠EGA,
∴∠DBA+∠BAD=∠EGA+∠BAD,
∴∠BDA=∠PFA,
∵AF⊥EP,
∴∠PFA=90°.
∴∠BDA=90°,
∴AB为圆的直径;
(2)证明:连接BC,DC,则
∵AB为圆的直径,
∴∠BDA=∠ACB=90°,
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
∴Rt△BDA≌Rt△ACB,
∴∠DAB=∠CBA,
∵∠DCB=∠DAB,
∴∠DCB=∠CBA,
∴DC∥AB,
∵AB⊥EP,
∴DC⊥EP,
∴∠DCE为直角,
∴ED为圆的直径,
∵AB为圆的直径,
∴AB=ED.
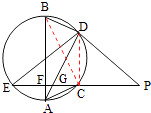
【解析】(1)证明AB为圆的直径,只需证明∠BDA=90°;(2)证明Rt△BDA≌Rt△ACB,再证明∠DCE为直角,即可证明AB=ED.

练习册系列答案
相关题目